题目内容
9．计算：3x-4x=-x；$\frac{1}{2}$y-3y+2y=-$\frac{1}{2}$y；-8x2+8x2=0．分析 先根据同类项的概念进行判断是否是同类项，然后根据合并同类项的法则，即系数相加作为系数，字母和字母的指数不变计算进行判断．
解答 解：3x-4x=-x；$\frac{1}{2}$y-3y+2y=-$\frac{1}{2}$y；-8x2+8x2=0，
故答案为：-x，-$\frac{1}{2}$y，0．
点评 本题主要考查的是同类项的概念和合并同类项的法则，掌握合并同类项的法则：系数相加作为系数，字母和字母的指数不变．
练习册系列答案
相关题目
19．定理“等腰三角形的两个底角相等”的逆定理是（ ）
| A． | 有两个角相等的三角形是等腰三角形 | |
| B． | 有两个底角相等的三角形是等腰三角形 | |
| C． | 有两个角不相等的三角形不是等腰三角形 | |
| D． | 不是等腰三角形的两个角不相等 |
20．顶点为（-6，0），开口向下，形状与函数y=$\frac{1}{2}$x2的图象相同的抛物线所对应的函数是（ ）
| A． | y=$\frac{1}{2}$（x-6）2 | B． | y=$\frac{1}{2}$（x+6）2 | C． | y=-$\frac{1}{2}$（x-6）2 | D． | y=-$\frac{1}{2}$（x+6）2 |
14．平面直角坐标系中，已知A（8，0），△AOP为等腰三角形且面积为16，满足条件的P点有（ ）
| A． | 12个 | B． | 10个 | C． | 8个 | D． | 6个 |
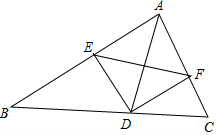如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ADC的高，下列说法中正确的有（ ）个
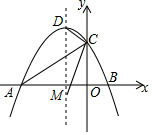如图，抛物线y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2与x轴交于A、B两点，与y轴交于C点，D为抛物线的顶点，M为抛物线对称轴上一点，当∠ACD=∠BCM时，求M点坐标．