题目内容
3.通分:(1)$\frac{x}{6a{b}^{2}}$,$\frac{y}{9{a}^{2}bc}$
(2)$\frac{a-1}{{a}^{2}+2a+1}$,$\frac{6}{{a}^{2}-1}$
(3)$\frac{1}{x}$,$\frac{x}{x+1}$,$\frac{2}{3x}$.
分析 (1)先确定最简公分母,再利用分式的性质求解即可;
(2)先因式分解,再确定最简公分母,再利用分式的性质求解即可;
(3)先确定最简公分母,再利用分式的性质求解即可.
解答 解:(1)$\frac{x}{6a{b}^{2}}$=$\frac{3xac}{18{a}^{2}{b}^{2}c}$,
$\frac{y}{9{a}^{2}bc}$=$\frac{2yb}{18{a}^{2}{b}^{2}c}$;
(2)$\frac{a-1}{{a}^{2}+2a+1}$=$\frac{a-1}{(a+1)^{2}}$=$\frac{(a-1)^{2}}{(a+1)^{2}(a-1)}$=$\frac{{a}^{2}-2a+1}{(a+1)^{2}(a-1)}$,
$\frac{6}{{a}^{2}-1}$=$\frac{6}{(a+1)(a-1)}$=$\frac{6(a+1)}{(a+1)^{2}(a-1)}$=$\frac{6a+6}{(a+1)^{2}(a-1)}$;
(3)$\frac{1}{x}$=$\frac{3(x+1)}{3x(x+1)}$=$\frac{3x+3}{3x(x+1)}$,
$\frac{x}{x+1}$=$\frac{3{x}^{2}}{3x(x+1)}$,
$\frac{2}{3x}$=$\frac{2(x+1)}{3x(x+1)}$=$\frac{2x+2}{3x(x+1)}$.
点评 本题考查了通分,解题的关系是准确找出最简公分母以及因式分解是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
13.实数16的平方根是( )
| A. | 4 | B. | ±4 | C. | 2$\sqrt{2}$ | D. | ±2$\sqrt{2}$ |
14.平面直角坐标系中,已知A(8,0),△AOP为等腰三角形且面积为16,满足条件的P点有( )
| A. | 12个 | B. | 10个 | C. | 8个 | D. | 6个 |
15.下列判断正确的是( )
| A. | a的系数为0 | B. | ab2c的次数是2 | ||
| C. | $\frac{1}{2}$πxy3的系数为$\frac{1}{2}$π | D. | -5是一次单项式 |
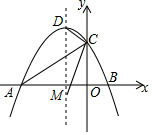 如图,抛物线y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2与x轴交于A、B两点,与y轴交于C点,D为抛物线的顶点,M为抛物线对称轴上一点,当∠ACD=∠BCM时,求M点坐标.
如图,抛物线y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2与x轴交于A、B两点,与y轴交于C点,D为抛物线的顶点,M为抛物线对称轴上一点,当∠ACD=∠BCM时,求M点坐标.