题目内容
5.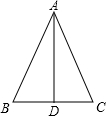 如图,已知AD是△ABC的中线,AB=AC,求证:
如图,已知AD是△ABC的中线,AB=AC,求证:(1)AD是△ABC的角平分线;
(2)AD⊥BC.
分析 (1)关键等腰三角形的性质得到∠B=∠C,推出△ABD≌△ACD,得到∠BAD=∠CAD,即可得到结论;
(2)由于△ABD≌△ACD,得到∠ADB=∠ADC,于是得到∠ADB=∠ADC=90°,即可得到结果.
解答 证明:(1)∵AB=AC,
∴∠B=∠C,
在△ABD与△ACD中,$\left\{\begin{array}{l}{AB=AC}\\{∠B=∠C}\\{BD=CD}\end{array}\right.$,
∴△ABD≌△ACD,
∴∠BAD=∠CAD,
∴AD是△ABC的角平分线;
(2)∵△ABD≌△ACD,
∴∠ADB=∠ADC,
∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,
∴AD⊥BC.
点评 本题考查了等腰三角形的性质,全等三角形的判定和性质,熟练掌握全等三角形的判定和性质定理是解题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
15.某班为了奖励在校运会上获得好成绩的运动员,花了200元钱购买甲乙两种奖品共30件,其中甲种奖品8元/件,乙种奖品6元/件.若设购买甲种奖品x件,乙种奖品y件,则所列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{8x+6y=30}\\{x+y=200}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{6x+8y=30}\\{x+y=200}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=30}\\{8x+6y=200}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=30}\\{6x+8y=200}\end{array}\right.$ |
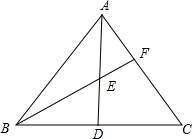 如图,AD是△ABC的中线,E为AD的中点,连接BE并延长,交AC于F,AF=$\frac{1}{3}$AC.求证:EF=$\frac{1}{4}$BF.
如图,AD是△ABC的中线,E为AD的中点,连接BE并延长,交AC于F,AF=$\frac{1}{3}$AC.求证:EF=$\frac{1}{4}$BF.