题目内容
16.将下列各式因式分解:(1)25(a+b)2-16(a-b)2;
(2)4(m-n)2-9(m+n)2;
(3)9(a-b)2+12(a2-b2)+4(a+b)2;
(4)x2y(x-y)2-2xy(y-x)3.
分析 (1)原式利用平方差公式分解即可;
(2)原式利用平方差公式分解即可;
(3)原式利用完全平方公式分解即可;
(4)原式提取公因式,即可得到结果.
解答 解:(1)原式=[5(a+b)+4(a-b)][5(a+b)-4(a-b)]=(9a+b)(a+9b);
(2)原式=[2(m-n)+3(m+n)][2(m-n)-3(m+n)]=-(5m+n)(m+5n);
(3)原式=[3(a-b)+2(a+b)]2=(5a-b)2;
(4)原式=xy(x-y)2[x+2(x-y)]=xy(x-y)2(3x-2y).
点评 此题考查了因式分解-运用公式法,熟练掌握公式解本题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
14.在△ABC中,AB=2,AC=3,$\overrightarrow{AB}$•$\overrightarrow{BC}$=1,则BC=( )
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{23}$ |
 如图,若三角形内角和为180°且∠C+∠A=∠AEC,判断AB与CD是否平行,并说明理由.
如图,若三角形内角和为180°且∠C+∠A=∠AEC,判断AB与CD是否平行,并说明理由.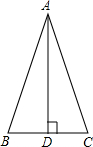 如图,AD是△ABC的高,若AB+BD=AC+CD,求证:△ABC是等腰三角形.
如图,AD是△ABC的高,若AB+BD=AC+CD,求证:△ABC是等腰三角形.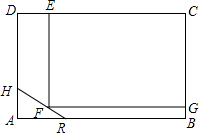 为实现城市绿化,某房地产公司要在拆迁地矩形ABCD(如图)上规划出一块矩形公园CEFG,但不能超过文物保护区△AHR的红线HR.已知AB=210cm,AD=140cm,AR=60cm,AH=40cm,那么当边CE多长时才能使公园CEFG占地面积最大?并求出最大面积.
为实现城市绿化,某房地产公司要在拆迁地矩形ABCD(如图)上规划出一块矩形公园CEFG,但不能超过文物保护区△AHR的红线HR.已知AB=210cm,AD=140cm,AR=60cm,AH=40cm,那么当边CE多长时才能使公园CEFG占地面积最大?并求出最大面积.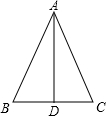 如图,已知AD是△ABC的中线,AB=AC,求证:
如图,已知AD是△ABC的中线,AB=AC,求证: