题目内容
13.已知$\frac{m}{n}$=$\frac{1}{2}$,求$\frac{m}{m-n}$-$\frac{n}{m+n}$+$\frac{2mn}{{m}^{2}-{n}^{2}}$的值.分析 根据已知条件得到n=2m,将其代入所求的代数式进行化简求值.
解答 解:由$\frac{m}{n}$=$\frac{1}{2}$,得n=2m,
则$\frac{m}{m-n}$-$\frac{n}{m+n}$+$\frac{2mn}{{m}^{2}-{n}^{2}}$
=$\frac{{m}^{2}-mn-mn+{n}^{2}+2mn}{{m}^{2}-{n}^{2}}$
=$\frac{{m}^{2}+{n}^{2}}{{m}^{2}-{n}^{2}}$
=$\frac{{m}^{2}+4{m}^{2}}{{m}^{2}-4{m}^{2}}$
=-$\frac{5}{3}$,
即:$\frac{m}{m-n}$-$\frac{n}{m+n}$+$\frac{2mn}{{m}^{2}-{n}^{2}}$=-$\frac{5}{3}$.
点评 本题考查了分式的化简求值.解答此题的关键是把分式化到最简,然后代值计算.

练习册系列答案
相关题目
 如图,若三角形内角和为180°且∠C+∠A=∠AEC,判断AB与CD是否平行,并说明理由.
如图,若三角形内角和为180°且∠C+∠A=∠AEC,判断AB与CD是否平行,并说明理由.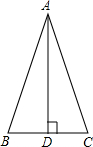 如图,AD是△ABC的高,若AB+BD=AC+CD,求证:△ABC是等腰三角形.
如图,AD是△ABC的高,若AB+BD=AC+CD,求证:△ABC是等腰三角形.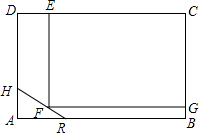 为实现城市绿化,某房地产公司要在拆迁地矩形ABCD(如图)上规划出一块矩形公园CEFG,但不能超过文物保护区△AHR的红线HR.已知AB=210cm,AD=140cm,AR=60cm,AH=40cm,那么当边CE多长时才能使公园CEFG占地面积最大?并求出最大面积.
为实现城市绿化,某房地产公司要在拆迁地矩形ABCD(如图)上规划出一块矩形公园CEFG,但不能超过文物保护区△AHR的红线HR.已知AB=210cm,AD=140cm,AR=60cm,AH=40cm,那么当边CE多长时才能使公园CEFG占地面积最大?并求出最大面积.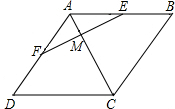 已知,如图,四边形ABCD是菱形,过AB的中点E作EF⊥AC于点M,交AD于点F,求证:AF=DF.
已知,如图,四边形ABCD是菱形,过AB的中点E作EF⊥AC于点M,交AD于点F,求证:AF=DF.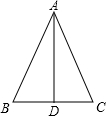 如图,已知AD是△ABC的中线,AB=AC,求证:
如图,已知AD是△ABC的中线,AB=AC,求证: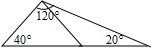 如图过三角形一个顶点画一条直线,把这个三角形分别分成两个等腰三角形.
如图过三角形一个顶点画一条直线,把这个三角形分别分成两个等腰三角形.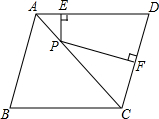 如图,在菱形ABCD中,点P是对角线AC上一点,PE⊥AD于点E,PF⊥CD于点F,若AB=5,菱形ABCD的面积为24,求PE+PF的值.
如图,在菱形ABCD中,点P是对角线AC上一点,PE⊥AD于点E,PF⊥CD于点F,若AB=5,菱形ABCD的面积为24,求PE+PF的值.