题目内容
 如图,在△ABC中,D是BC边上一点,且BA=BD,∠DAC=∠B,∠C=50°,求∠BAC的度数.
如图,在△ABC中,D是BC边上一点,且BA=BD,∠DAC=∠B,∠C=50°,求∠BAC的度数.考点:等腰三角形的性质
专题:
分析:用∠B表示出∠BAD,在△ABC中,根据三角形内角和定理得到关于∠B的方程,求得∠B,进一步求得∠BAC的度数.
解答:解:∵BA=BD,
∴∠BAD=(90°-
∠B),
在△ABC中,∠B+(90°-
∠B)+∠B+50°=180°,
解得∠B=
,
∠BAC=(90°-
∠B)+∠B=
.
故∠BAC的度数是
.
∴∠BAD=(90°-
| 1 |
| 2 |
在△ABC中,∠B+(90°-
| 1 |
| 2 |
解得∠B=
| 80° |
| 3 |
∠BAC=(90°-
| 1 |
| 2 |
| 310° |
| 3 |
故∠BAC的度数是
| 310° |
| 3 |
点评:考查了等腰三角形两底角相等的性质,三角形内角和定理,方程思想的应用.

练习册系列答案
相关题目
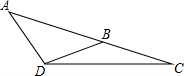 如图,在△ABC中,AD=BD=BC,若∠C=25°,则∠ADB的度数是( )
如图,在△ABC中,AD=BD=BC,若∠C=25°,则∠ADB的度数是( )| A、50° | B、60° |
| C、80° | D、90° |
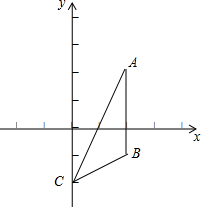 如图,点A、B、C的坐标分别是(2,2),(2,-1),(0,-2).
如图,点A、B、C的坐标分别是(2,2),(2,-1),(0,-2). 一辆卡车装满货物后,它的高比宽多两米,且恰好通过如图所示的隧道,(上部为半圆形).卡车有多高?(结果精确到0.1m).
一辆卡车装满货物后,它的高比宽多两米,且恰好通过如图所示的隧道,(上部为半圆形).卡车有多高?(结果精确到0.1m).