题目内容
已知a、b、c是△ABC的三边,化简
-2
+3|a+b-c|.
| (a-b-c)2 |
| a2+b2+c2-2ab-2bc+2ac |
考点:二次根式的性质与化简,三角形三边关系
专题:
分析:根据三角形的三边关系得出b+c>a,a+b>c,根据二次根式的性质得出|a-b-c|-2|a-b-c|+3|a+b-c|,去掉绝对值符号求出即可.
解答:解:∵a、b、c是△ABC的三边,
∴b+c>a,a+b>c,
∴
-2
+3|a+b-c|
=|a-b-c|-2|a-b-c|+3|a+b-c|
=b+c-a-2(b+c-a)+3(a+b-c)
=b+c-a-2b-2c+2a+3a+3b-3c
=4a+2b-4c.
∴b+c>a,a+b>c,
∴
| (a-b-c)2 |
| a2+b2+c2-2ab-2bc+2ac |
=|a-b-c|-2|a-b-c|+3|a+b-c|
=b+c-a-2(b+c-a)+3(a+b-c)
=b+c-a-2b-2c+2a+3a+3b-3c
=4a+2b-4c.
点评:本题考查了三角形三边关系定理,二次根式的性质,绝对值的应用,解此题的关键是得出原式=b+c-a-2b-2c+2a+3a+3b-3c.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
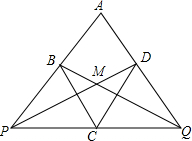 如图,菱形ABCD中,∠A=60°,过顶点C任意作一直线分别交AB、AD的延长线于P、Q两点,设PD、QB相交于点M.求证:∠PMQ=120°.
如图,菱形ABCD中,∠A=60°,过顶点C任意作一直线分别交AB、AD的延长线于P、Q两点,设PD、QB相交于点M.求证:∠PMQ=120°. 如图,在△ABC与△DEF中,AB=DE,∠B=∠E,AC=DF,判断△ABC与△DEF是否全等,并说明理由.
如图,在△ABC与△DEF中,AB=DE,∠B=∠E,AC=DF,判断△ABC与△DEF是否全等,并说明理由. 如图,在△ABC中,D是BC边上一点,且BA=BD,∠DAC=∠B,∠C=50°,求∠BAC的度数.
如图,在△ABC中,D是BC边上一点,且BA=BD,∠DAC=∠B,∠C=50°,求∠BAC的度数.