题目内容
2．
邮递员从邮局出发，分别到村庄A、B、C投递邮件，其所走的顺序为邮局A→B→C→邮局，则邮局应建在公路l的何位置，可使邮递员走的路程最短？
分析 A、B、C三点的距离是不变的，则邮递员走的路程最短，则只需要A、C到公路的距离和最短，由对称性知识可知，可在公路上找到一点到A、C的距离之和最短即可，作点A关于直线l的对称点A′，连接A′C与直线l交于点D，则点D即为所求．
解答 
解：由题意可知：A、B、C三点的距离是不变的，则要使送货路程最短，则只需要A、C到公路的距离之和最短，由对称性知识可知，可在公路上找到一点到A、C的距离之和最短的点就可，如图所示，点D即为所求．
点评 本题考查轴对称-最短路线问题，熟知两点之间线段最短是解答此题的关键．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
13．
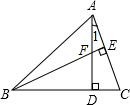如图，AD，BE为△ABC的两条高，∠1=30°，则下列结论不正确的是（ ）
如图，AD，BE为△ABC的两条高，∠1=30°，则下列结论不正确的是（ ）| A． | AC=2CD | B． | BC=2CE | C． | CD=CE | D． | AF=2EF |
如图，等边三角形ABC内接于⊙O，D是AB上的一点，则∠ADB=120°．
如图，已知抛物线y=ax2+bx+3经过点B（3，0），C（4，3），与y轴交于点A，把抛物线向上平移，使得顶点E落在x轴上点F处，点A平移至点D处，则两条抛物线、对称轴EF和y轴围成的图形（图中阴影部分）的面积S=2．
14．下列因式分解错误的是 （ ）
| A． | -$\frac{1}{2}$+8x2=-$\frac{1}{2}$（1-4x）（1+4x） | B． | 16x2-4=（4x+2）（4x-2） | ||
| C． | m2+m+$\frac{1}{4}$=（m+$\frac{1}{2}$）2 | D． | -x2+4y2=（x+2y）（2y-x） |
有理数a、b、c在数轴上的位置如图所示，化简|a+2b|-|3b+c|+|b-a|-|4-2c|．
已知：如图，△ABC中，D、E是BC上两点，AB=AC，AD=AE，BD=CE．求证：∠BAE=∠CAD．