题目内容
2. 如图,△ABC的面积为4cm2,D为AC的中点,则图中两块阴影部分的面积和为2cm2.
如图,△ABC的面积为4cm2,D为AC的中点,则图中两块阴影部分的面积和为2cm2.
分析 连结BD,如图,先证明△AED∽△ABC,利用相似比得到AB=2AE,即AE=BE,根据三角形面积公式得到S△ADE=S△BDE,同理可得S△CDF=S△BDF,于是得到两块阴影部分的面积和=$\frac{1}{2}$S△ABC=2cm2.
解答 解: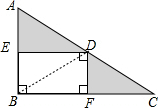 连结BD,如图,
连结BD,如图,
∵DE∥BC,
∴△AED∽△ABC,
∴AE:BAB=AD:AC,
∵D为AC的中点,
∴AC=2AD,
∴AB=2AE,即AE=BE,
∴S△ADE=S△BDE,
同理可得S△CDF=S△BDF,
∴两块阴影部分的面积和=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×4=2(cm2).
故答案为2.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;在利用相似三角形的性质时主要利用相似比计算线段的长.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
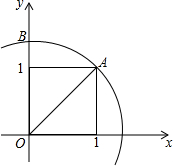 如图,平面直角坐标中,以x轴上一个单位长度为边长画一个正方形,以原点为圆心,正方形的对角线OA为半径画弧,与y轴正半轴的交点B表示的坐标是(0,$\sqrt{2}$).
如图,平面直角坐标中,以x轴上一个单位长度为边长画一个正方形,以原点为圆心,正方形的对角线OA为半径画弧,与y轴正半轴的交点B表示的坐标是(0,$\sqrt{2}$).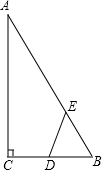 如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC中点.若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为2秒或3.5秒或4.5秒.
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC中点.若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为2秒或3.5秒或4.5秒. 已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c-$\frac{1}{x}$=0的根的情况是有一个正根.
已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c-$\frac{1}{x}$=0的根的情况是有一个正根.