题目内容
12.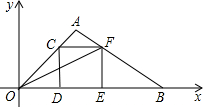 在直角坐标系中,O为坐标原点,点A的坐标为(1,1),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,若以B,E,F为顶点的三角形与△OFE相似,B点的坐标是($\frac{3}{2}$,0)(3,0).
在直角坐标系中,O为坐标原点,点A的坐标为(1,1),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,若以B,E,F为顶点的三角形与△OFE相似,B点的坐标是($\frac{3}{2}$,0)(3,0).
分析 根据点A坐标是(1,1)可以确定∠AOB=45°,又四边形CDEF是正方形,所以0D=CD=DE,即可证明△OFE的边OE=2EF,再根据“以B,E,F为顶点的三角形与△OFE相似”分①EF=2EB,②EB=2EF两种情况讨论,根据△ACF与△AOB相似,相似三角形对应高的比等于对应边的比列出比例式计算即可求出正方形的边长,从而OB的长亦可求出.
解答 解:过点A作AH⊥OB,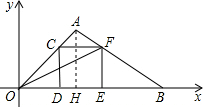
∵点A的坐标为(1,1),
∴AH=OH=1,∠AOB=45°,
∴OD=CD,
设CF=x,
∵四边形CDEF是正方形,
∴CF∥DE,CD=CF=EF=DE,
∴CD=CF=EF=DE=x,
∴OE=OD+DE=2EF,
∵以B,E,F为顶点的三角形与△OFE相似,
∴①EF=2EB,则EB=0.5x,
∴OB=OE+EB=2x+0.5x=2.5x,
∵CF∥DE,
∴△ACF∽△AOB,
∴$\frac{CF}{OB}$=$\frac{1-x}{1}$,
即$\frac{x}{\frac{5}{2}x}$=1-x,
解得x=$\frac{3}{5}$,
OB=$\frac{5}{2}$×$\frac{3}{5}$=1.5,
∴点B的坐标为(1.5,0),
②EB=2EF时,则EB=2x,
∴OB=OE+EB=2x+2x=4x,
∵CF∥DE,
∴△ACF∽△AOB,
∴$\frac{CF}{OB}$=$\frac{1-x}{1}$,
即$\frac{x}{4x}$=1-x,
解得x=$\frac{3}{4}$,
OB=4x=4×$\frac{3}{4}$=3,
∴点B的坐标为(3,0).
综上所述,点B的坐标是(1.5,0)或(3,0).
故答案为:($\frac{3}{2}$,0)(3,0).
点评 此题考查了相似三角形的性质对应高的比等于对应边的比的性质,解题的关键是根据点A的坐标(1,1)确定出OE=2EF,注意要分情况讨论,避免漏解.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案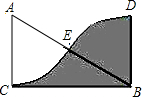 如图,△ABC中,∠C=90°,BC=$2\sqrt{3}$,若扇形ACE与扇形BDE关于点E中心对称,则图中阴影部分的面积为( )
如图,△ABC中,∠C=90°,BC=$2\sqrt{3}$,若扇形ACE与扇形BDE关于点E中心对称,则图中阴影部分的面积为( )| A. | 2 | B. | $2\sqrt{3}$ | C. | 4 | D. | $4\sqrt{3}$ |
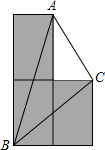 用3块形状、大小先完全相同的长方形小木片,拼成知图所示的“L”形,点A,B,C分别是其中的3个顶点,若AB=8cm,CB=6cm,则AC=2$\sqrt{5}$cm.
用3块形状、大小先完全相同的长方形小木片,拼成知图所示的“L”形,点A,B,C分别是其中的3个顶点,若AB=8cm,CB=6cm,则AC=2$\sqrt{5}$cm.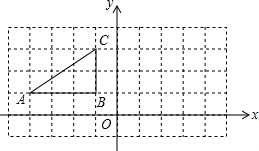 如图,方格纸中的每个小方格都是边长为1个单位的正方形.Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(-4,1),点B的坐标为(-1,1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形.Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(-4,1),点B的坐标为(-1,1).