题目内容
14.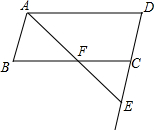 一个平行四边形ABCD,AB=4,BC=9,点E是DC延长线上一点,连接AE交BC边于点F,求BF+EC的最小值.
一个平行四边形ABCD,AB=4,BC=9,点E是DC延长线上一点,连接AE交BC边于点F,求BF+EC的最小值.
分析 设BF=x,EC=y,由AB∥DE,推出$\frac{AB}{CE}$=$\frac{BF}{CF}$,即$\frac{4}{y}$=$\frac{x}{9-x}$,可得y=$\frac{36}{x}$-4,推出BF+EC=x+y=x+$\frac{36}{x}$-4,由($\sqrt{x}$-$\sqrt{\frac{36}{x}}$)2≥0,推出x-12+$\frac{36}{x}$≥0,推出x+$\frac{36}{x}$≥12,推出BF+EC≥12-4,即BF+EC≥8,由此即可解决问题.
解答  解:设BF=x,EC=y,
解:设BF=x,EC=y,
∵四边形ABCD是平行四边形,
∴AB∥DE,
∴$\frac{AB}{CE}$=$\frac{BF}{CF}$,
∴$\frac{4}{y}$=$\frac{x}{9-x}$,
∴y=$\frac{36}{x}$-4,
∴BF+EC=x+y=x+$\frac{36}{x}$-4,
∵($\sqrt{x}$-$\sqrt{\frac{36}{x}}$)2≥0,
∴x-12+$\frac{36}{x}$≥0,
∴x+$\frac{36}{x}$≥12,
∴BF+EC≥12-4,
∴BF+EC≥8,
∴BF+EC的最小值为8.
点评 本题考查平行四边形的性质、最短问题、完全平方公式等知识,解题的关键是学会利用参数,构建函数解决最值问题,题目比较难,证明x+$\frac{36}{x}$≥12是本题的突破点.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
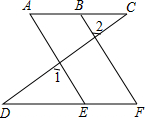 如图,∠1=∠2,∠A=∠F,求证:∠C=∠D.
如图,∠1=∠2,∠A=∠F,求证:∠C=∠D.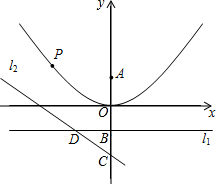 如图,在平面直角坐标系中,直线l1过点B(0,-1),且平行于x轴,直线l2过点C(0,-2),交直线l1于点D,$\frac{BD}{BC}=\frac{4}{3}$,点A与点B关于x轴对称,点P为抛物线y=$\frac{1}{4}$x2上一动点,PQ⊥l1于点Q.
如图,在平面直角坐标系中,直线l1过点B(0,-1),且平行于x轴,直线l2过点C(0,-2),交直线l1于点D,$\frac{BD}{BC}=\frac{4}{3}$,点A与点B关于x轴对称,点P为抛物线y=$\frac{1}{4}$x2上一动点,PQ⊥l1于点Q.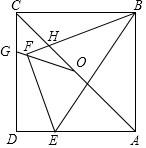 在正方形ABCD中,AB=6,点E在边AD上,DE=$\frac{1}{3}$AD.连接BE,将△ABE沿BE翻折,点A落在点F处,BF与AC交于点H,点O是AC的中点,连接OF并延长交CD于点G,则四边形GFHC的面积是$\frac{5184}{2431}$.
在正方形ABCD中,AB=6,点E在边AD上,DE=$\frac{1}{3}$AD.连接BE,将△ABE沿BE翻折,点A落在点F处,BF与AC交于点H,点O是AC的中点,连接OF并延长交CD于点G,则四边形GFHC的面积是$\frac{5184}{2431}$. 如图,在四边形ABCD中,AD∥BC,∠B=90度,AD=18cm,BC=21cm,动点P从A点开始沿AD边向D以1cm/s的速度运动,动点Q从C点开始沿CB边以2cm/s的速度运动,P、Q分别从点A、C同时出发.当其中一点到达端点时,另一点也随之停止运动,设运动的时间为t秒.
如图,在四边形ABCD中,AD∥BC,∠B=90度,AD=18cm,BC=21cm,动点P从A点开始沿AD边向D以1cm/s的速度运动,动点Q从C点开始沿CB边以2cm/s的速度运动,P、Q分别从点A、C同时出发.当其中一点到达端点时,另一点也随之停止运动,设运动的时间为t秒.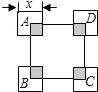 如图,大正方形ABCD的边长为8,四个全等的小正方形的对称中心分别在大正方形的四个顶点上,且它们的各边与正方形各边平行或垂直.若小正方形的边长为(0<x≤8),重叠部分的面积为y,能反映y与x之间函数关系的大致图象是( )
如图,大正方形ABCD的边长为8,四个全等的小正方形的对称中心分别在大正方形的四个顶点上,且它们的各边与正方形各边平行或垂直.若小正方形的边长为(0<x≤8),重叠部分的面积为y,能反映y与x之间函数关系的大致图象是( )