题目内容
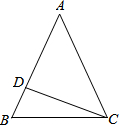 在等腰△ABC中,AB=AC,CD⊥AB于D.
在等腰△ABC中,AB=AC,CD⊥AB于D.(1)若∠A=40°,求∠DBC的度数;
(2)若AB=15,CD=9,求BD的长.
考点:等腰三角形的性质,勾股定理
专题:
分析:(1)根据三角形的内角和定理即可求得;
(2)分两种情况考虑:三角形ABC为锐角三角形,如图1所示;三角形ABC为钝角三角形,如图2所示,分别求出BD的长即可.
(2)分两种情况考虑:三角形ABC为锐角三角形,如图1所示;三角形ABC为钝角三角形,如图2所示,分别求出BD的长即可.
解答:解:(1)∵AB=AC,
∴∠B=∠ACB,
∵∠A=40°,
∴∠DBC=70°;
(2)当△ABC为锐角三角形时,如图1所示,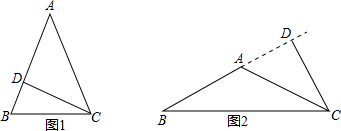
在Rt△ACD中,AC=AB=15,CD=9,
根据勾股定理得:AD=
=12,
此时BD=AB-AD=15-12=3;
当△ABC为钝角三角形时,如图2所示,
在Rt△ACD中,CD=9,AC=AB=15,
根据勾股定理得:AD=
=12,
此时BD=AB+BD=15+12=27.
所以BD的长为3或27.
∴∠B=∠ACB,
∵∠A=40°,
∴∠DBC=70°;
(2)当△ABC为锐角三角形时,如图1所示,

在Rt△ACD中,AC=AB=15,CD=9,
根据勾股定理得:AD=
| AC2-CD2 |
此时BD=AB-AD=15-12=3;
当△ABC为钝角三角形时,如图2所示,
在Rt△ACD中,CD=9,AC=AB=15,
根据勾股定理得:AD=
| AC2-CD2 |
此时BD=AB+BD=15+12=27.
所以BD的长为3或27.
点评:此题考查了等腰三角形的性质以及勾股定理,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
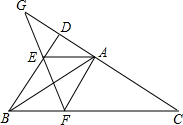 在△ABC中,以边AB为轴翻折∠ABC,使翻折后BC的对应边交CA的延长线于点D.分别过A作AE∥BC交BD于E,作AF∥BD交BC于F,延长CD、EF交于G.若BC=2BD,BE=1,求DE的长
在△ABC中,以边AB为轴翻折∠ABC,使翻折后BC的对应边交CA的延长线于点D.分别过A作AE∥BC交BD于E,作AF∥BD交BC于F,延长CD、EF交于G.若BC=2BD,BE=1,求DE的长 如图,AB是⊙O的直径,点C在⊙O上,AB=6,∠B=30°,则BC的长为( )
如图,AB是⊙O的直径,点C在⊙O上,AB=6,∠B=30°,则BC的长为( )| A、12 | ||
B、3
| ||
C、2
| ||
D、12
|