题目内容
若|a-1|+(ab-2)2=0,则方程
+
+
+…+
=2002的解是 .
| x |
| ab |
| x |
| (a+1)(b+1) |
| x |
| (a+2)(b+2) |
| x |
| (a+2001)(b+2001) |
考点:解一元一次方程,非负数的性质:绝对值,非负数的性质:偶次方
专题:计算题
分析:利用非负数的性质求出a与b的值,代入方程计算即可求出解.
解答:解:∵|a-1|+(ab-2)2=0,
∴a-1=0,ab-2=0,
解得:a=1,b=2,
已知方程变形得:(
+
+…+
)x=2002,
整理得:(1-
+
-
+…+
-
)x=2002,
即
x=2002,
解得:x=2003.
故答案为:x=2003.
∴a-1=0,ab-2=0,
解得:a=1,b=2,
已知方程变形得:(
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 2002×2003 |
整理得:(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2002 |
| 1 |
| 2003 |
即
| 2002 |
| 2003 |
解得:x=2003.
故答案为:x=2003.
点评:此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
某班学生每周课外阅读时间的统计结果如下表:则这些学生每周课外阅读的平均时间为( )
| 时间/小时 | 3 | 4 | 5 | 6 | 7 |
| 人数 | 2 | 5 | 15 | 11 | 7 |
| A、4.5小时 | B、5小时 |
| C、5.4小时 | D、5.5小时 |
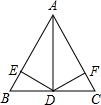 如图,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,则下列四个结论中:①DE=DF; ②AD上任意一点到AB、AC的距离相等; ③∠BDE=∠CDF;④BD=CD,AD⊥BC.其中正确的有( )
如图,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,则下列四个结论中:①DE=DF; ②AD上任意一点到AB、AC的距离相等; ③∠BDE=∠CDF;④BD=CD,AD⊥BC.其中正确的有( )| A、1个 | B、2个 | C、3个 | D、4个 |
已知x-y=3,x2-y2=12,那么x+y的值是( )
| A、3 | B、4 | C、6 | D、12 |
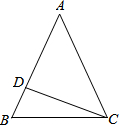 在等腰△ABC中,AB=AC,CD⊥AB于D.
在等腰△ABC中,AB=AC,CD⊥AB于D. 如图,将两张长为8,宽为2的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的周长有最小值8,那么菱形周长的最大值是( )
如图,将两张长为8,宽为2的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的周长有最小值8,那么菱形周长的最大值是( )