题目内容
7. 如图,在?ABCD中,AD=3cm,AB=5cm,BD=4cm,求?ABCD的面积及对角线AC的长.
如图,在?ABCD中,AD=3cm,AB=5cm,BD=4cm,求?ABCD的面积及对角线AC的长.
分析 由AD=3cm,AB=5cm,BD=4cm,利用勾股定理的逆定理即可判定AD⊥BD,即可求得?ABCD的面积,然后利用平行四边形的对角线互相平分,求得OD的长,再利用勾股定理,求得OA的长,继而求得答案.
解答 解:∵AD=3cm,AB=5cm,BD=4cm,
∴AD2+BD2=AB2,
∴∠ADB=90°,
∴S?ABCD=AD•BD=3×4=12(cm2);
∵四边形ABCD是平行四边形,
∴OD=$\frac{1}{2}$BD=2cm,AC=2OA,
∵OA=$\sqrt{A{D}^{2}+O{D}^{2}}$=$\sqrt{13}$(cm),
∴AC=2OA=2$\sqrt{13}$cm.
点评 此题考查了平行四边形的性质以及勾股定理与逆定理.注意判定AD⊥BD是关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
17.一元二次方程x2+x+$\frac{1}{4}$=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
15. 实数a在数轴上的位置如图所示,则下列说法不正确的是( )
实数a在数轴上的位置如图所示,则下列说法不正确的是( )
 实数a在数轴上的位置如图所示,则下列说法不正确的是( )
实数a在数轴上的位置如图所示,则下列说法不正确的是( )| A. | a的相反数大于2 | B. | a的相反数是2 | C. | |a|>2 | D. | 2a<0 |
12.已知点M(4,2),N(1,1),点P是x轴上一动点,若使PM+PN最短,则点P为( )
| A. | (2,0) | B. | (2.5,0) | C. | (3,0) | D. | (4,0) |
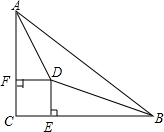 如图所示△ABC中,∠C=90°,∠A,∠B的平分线交于D点,DE⊥BC于点E,DF⊥AC于点F.
如图所示△ABC中,∠C=90°,∠A,∠B的平分线交于D点,DE⊥BC于点E,DF⊥AC于点F.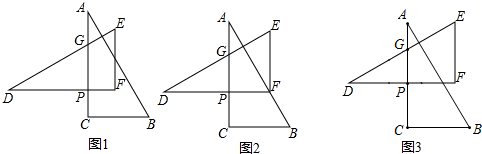
 如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,以AB为直径作⊙O恰好与CD相切.
如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,以AB为直径作⊙O恰好与CD相切.