题目内容
17.如图,正方形ABCD中对角线AC、BD相交于点O,(1)在图1中E是AC上一点,F是OB上一点,且OE=OF,回答下列问题:可以通过平移、旋转、翻折中的哪一种方法,如何变换使△OAF变到△OBE的位置?答:以点O为旋转中心,逆时针旋转90度.
(2)若点E、F分别在OC、OB的延长线上,并且OE=OF(如图2),试比较AF与BE长度的大小并说明理由.
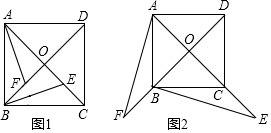
分析 (1)根据图形特点即可得到答案;
(2)延长AF交BE于M,根据正方形性质求出AB=BC,∠AOB=∠BOC,证△AOF≌△BOE,推出AF=BE.
解答  解:(1)旋转,以点O为旋转中心,逆时针旋转90度.
解:(1)旋转,以点O为旋转中心,逆时针旋转90度.
故答案是:以点O为旋转中心,逆时针旋转90度.
(2)图(1)中AF和BE之间的关系:AF=BE;AF⊥BE.
证明:如图2,延长EB交AF于M,
∵四边形ABCD是正方形,
∴AC⊥BD,OA=OB,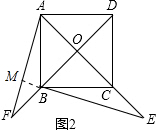
∴∠AOB=∠BOC=90°,
在△AOF和△BOE中$\left\{\begin{array}{l}{AO=OB}\\{∠AOF=∠BOE}\\{OF=OE}\end{array}\right.$,
∴△AOF≌△BOE(SAS),
∴AF=BE.
点评 本题主要考查对正方形的性质,全等三角形的性质和判定,旋转的性质等知识点的连接和掌握,综合运用这些性质进行推理是解此题的关键.

练习册系列答案
相关题目
6.正方形ABCD所在平面内有一点P,使△PAB、△PBC、△PCD、△PDA都是等腰三角形,那么具有这样性质的点P共有( )
| A. | 5个 | B. | 7个 | C. | 8个 | D. | 9个 |
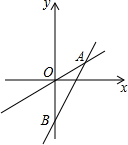 如图表示一个正比例函数y1=k1x与一个一次函数y2=k2x+b的图象,它们交于点
如图表示一个正比例函数y1=k1x与一个一次函数y2=k2x+b的图象,它们交于点