题目内容
7．已知|a-1|与（b+2）2互为相反数，求（a+b）2015+a2016的值．分析 根据相反数的概念列出算式，根据非负数的性质求出a、b的值，计算即可．
解答 解：由题意得，|a-1|+（b+2）2，=0，
则a-1=0，b+2=0，
解得，a=1，b=-2，
则（a+b）2015+a2016=-1+1=0．
点评 本题考查的是非负数的性质，掌握当几个非负数相加和为0时，则其中的每一项都必须等于0是解题的关键．
练习册系列答案
相关题目
15．
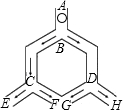如图，一个小球从A点沿制定的轨道下落，在每个交叉口都有向左或向右两种机会均等的结果，小球最终到达H点的概率是（ ）
如图，一个小球从A点沿制定的轨道下落，在每个交叉口都有向左或向右两种机会均等的结果，小球最终到达H点的概率是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{3}$ |
19．若m，n为任意实数，则下列各式成立的是（ ）
| A． | $\sqrt{（m+n）^{2}}$=m+n | B． | $\sqrt{{m}^{2}}$+$\sqrt{{n}^{2}}$=m+n | C． | $\sqrt{mn}$=$\sqrt{m}+\sqrt{n}$ | D． | $\sqrt{（m+n）^{4}}=（m+n）^{2}$ |
