题目内容
5．已知一次函数y=（m-3）x+m-8，y随x的增大而增大，（1）求m的取值范围；
（2）如果这个一次函数又是正比例函数，求m的值；
（3）如果这个一次函数的图象经过一、三、四象限，试写一个m的值，不用写理由．
分析 （1）根据函数的增减性得到m-3＞0，从而确定m的取值范围；
（2）根据正比例函数的定义得到m-3≠0且m-8=0，从而确定m的值；
（3）根据一次函数的性质确定m的取值范围，然后从m的范围内确定m的一个值即可．
解答 解：（1）根据题意得m-3＞0，
解得m＞3；
（2）根号题意得m-3≠0且m-8=0，
解得m=8；
（3）根据题意得：
$\left\{\begin{array}{l}{m-3＞0}\\{m-8＜0}\end{array}\right.$，
解得：3＜m＜8，
∴3＜m＜8中任取一个值都可以．
点评 本题考查了一次函数图象与系数的关系及正比例函数的定义，解题的关键是了解一次函数的性质，难度不大．
练习册系列答案
相关题目
15．
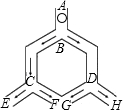如图，一个小球从A点沿制定的轨道下落，在每个交叉口都有向左或向右两种机会均等的结果，小球最终到达H点的概率是（ ）
如图，一个小球从A点沿制定的轨道下落，在每个交叉口都有向左或向右两种机会均等的结果，小球最终到达H点的概率是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{3}$ |
13．某树主干长出若干数目的支干，每个支干又长出同样数目小分支，主干、支干和小分支总数共73．若设主干长出x个支干，则可列方程是（ ）
| A． | （1+x）2=73 | B． | 1+x+x2=73 | C． | （1+x）x=73 | D． | 1+x+2x=73 |
20．某人去水果批发市场采购苹果，他看中了A、B两家苹果．这两家苹果品质都一样，零售价都为6元/千克，但批发价各不相同．
A家规定：批发数量不超过1000千克，按零售价的92%优惠；批发数量不超过2000千克，按零售价的90%优惠；超过2000千克的按零售价的88%优惠．
B家的规定如表：
【表格说明：批发价格分段计算，如：某人批发苹果2100千克，则总费用=6×95%×500+6×85%×1000+6×75%×（2100-1500）】
根据上述信息，请解答下列问题：
（1）如果他批发1000千克苹果，则他在A 家批发需要5520元，在B家批发需要5400元；
（2）如果他批发x千克苹果（1500＜x＜2000），则他在A 家批发需要5.4x元，在B家批发需要4.5x+1200元（用含x的代数式表示）；
（3）现在他要批发不超过1000千克苹果，你能帮助他选择在哪家批发更优惠吗？请说明理由．
A家规定：批发数量不超过1000千克，按零售价的92%优惠；批发数量不超过2000千克，按零售价的90%优惠；超过2000千克的按零售价的88%优惠．
B家的规定如表：
| 数量范围（千克） | 0～500 | 500以上～1500 | 1500以上～2500 | 2500以上 |
| 价 格（元） | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
根据上述信息，请解答下列问题：
（1）如果他批发1000千克苹果，则他在A 家批发需要5520元，在B家批发需要5400元；
（2）如果他批发x千克苹果（1500＜x＜2000），则他在A 家批发需要5.4x元，在B家批发需要4.5x+1200元（用含x的代数式表示）；
（3）现在他要批发不超过1000千克苹果，你能帮助他选择在哪家批发更优惠吗？请说明理由．
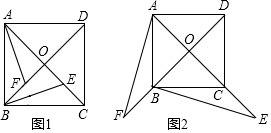
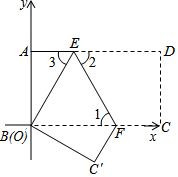如图．把长方形纸片ABCD沿EF折叠后，使得点D与点B重合，点C落在点C′的位置．