题目内容
18. 如图所示,在平面直角坐标系中,有若干个点按如下规律排列:(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),…,则第100个点的横坐标为( )
如图所示,在平面直角坐标系中,有若干个点按如下规律排列:(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),…,则第100个点的横坐标为( )| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
分析 设横坐标为n的点的个数为an,横坐标≤n的点的个数为Sn(n为正整数),结合图形找出部分an的值,根据数值的变化找出变化规律“an=n”,再罗列出部分Sn的值,根据数值的变化找出变化规律“Sn=$\frac{n(n+1)}{2}$”,依次变化规律解不等式100≤$\frac{n(n+1)}{2}$即可得出结论.
解答 解:设横坐标为n的点的个数为an,横坐标≤n的点的个数为Sn(n为正整数),
观察,发现规律:a1=1,a2=2,a3=3,…,
∴an=n.
S1=a1=1,S2=a1+a2=3,S3=a1+a2+a3=6,…,
∴Sn=1+2+…+n=$\frac{n(n+1)}{2}$.
当100≤Sn,即100≤$\frac{n(n+1)}{2}$,
解得:n≤-$\frac{1+2\sqrt{201}}{2}$(舍去),或n≥$\frac{2\sqrt{201}-1}{2}$.
∵13<$\frac{2\sqrt{201}-1}{2}$<14,
故选C.
点评 本题考查了规律型中得点的坐标的变化,解题的关键是找出变化规律“Sn=$\frac{n(n+1)}{2}$”.本题属于基础题,难道不大,解决该题型题目时,根据点的坐标的变化找出an、Sn的值,再根据数值的变化找出变化规律是关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
8. 如图,⊙O是△ABC的外接圆,已知∠C=60°,则∠BAO的度数是( )
如图,⊙O是△ABC的外接圆,已知∠C=60°,则∠BAO的度数是( )
 如图,⊙O是△ABC的外接圆,已知∠C=60°,则∠BAO的度数是( )
如图,⊙O是△ABC的外接圆,已知∠C=60°,则∠BAO的度数是( )| A. | 15° | B. | 30° | C. | 60° | D. | 120° |
9.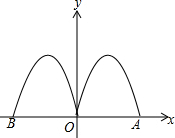 如图,抛物线y=-2x2+4x与x轴交于点O、A,把抛物线在x轴及其上方的部分记为C1,将C1以y铀为对称轴作轴对称得到C2,C2与x轴交于点B,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是( )
如图,抛物线y=-2x2+4x与x轴交于点O、A,把抛物线在x轴及其上方的部分记为C1,将C1以y铀为对称轴作轴对称得到C2,C2与x轴交于点B,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是( )
 如图,抛物线y=-2x2+4x与x轴交于点O、A,把抛物线在x轴及其上方的部分记为C1,将C1以y铀为对称轴作轴对称得到C2,C2与x轴交于点B,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是( )
如图,抛物线y=-2x2+4x与x轴交于点O、A,把抛物线在x轴及其上方的部分记为C1,将C1以y铀为对称轴作轴对称得到C2,C2与x轴交于点B,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是( )| A. | 0<m$<\frac{9}{8}$ | B. | $\frac{9}{8}$<m<$\frac{25}{8}$ | C. | 0<m<$\frac{25}{8}$ | D. | m<$\frac{9}{8}$或m<$\frac{25}{8}$ |
6.不等式的-x<2解集在数轴上表示如下,正确的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
13.如果一个多边形的内角和是1800°,这个多边形是( )
| A. | 八边形 | B. | 十四边形 | C. | 十边形 | D. | 十二边形 |
3. 如图,?ABCD中,BC=BD,∠C=72°,则∠ADB的度数是( )
如图,?ABCD中,BC=BD,∠C=72°,则∠ADB的度数是( )
 如图,?ABCD中,BC=BD,∠C=72°,则∠ADB的度数是( )
如图,?ABCD中,BC=BD,∠C=72°,则∠ADB的度数是( )| A. | 18° | B. | 26° | C. | 36° | D. | 72° |
10.下列成语所描述的事件是必然事件的是( )
| A. | 瓮中捉鳖 | B. | 守株待兔 | C. | 拔苗助长 | D. | 水中捞月 |
7.同样大小的黑色棋子按如图所示的规律摆放:

那么第671个图形中棋子的个数为( )

那么第671个图形中棋子的个数为( )
| A. | 2016 | B. | 2015 | C. | 2014 | D. | 2013 |
8. 如图是一个几何体的三视图,则这个几何体的侧面积是( )
如图是一个几何体的三视图,则这个几何体的侧面积是( )
 如图是一个几何体的三视图,则这个几何体的侧面积是( )
如图是一个几何体的三视图,则这个几何体的侧面积是( )| A. | 9π | B. | 18π | C. | 27π | D. | 36π |