题目内容
已知O为等边△ABC内的一点,OA=6,OB=8,OC=10,求△ABC的面积.
考点:旋转的性质,等边三角形的性质,勾股定理的逆定理
专题:
分析:将△AOB沿逆时针旋转至△ADC,将△AOC沿逆时针旋转至△BEC,将△BOC沿逆时针旋转至△BFA,得出OA=AD,∠OAB=∠DAC,OC=EC,∠OCB=∠ECB,从而得出△OAD是等边三角形,△ODC是直角三角形,即可得到S△OAD=
OA•
OA=
×6×
×6=9
,S△ODC=
OD•DC=
×6×8=24,得出S△OAB+S△OAC=S△OAD+,S△ODC=9
+24,同理得出S△OBC+S△OAC=S△OCE+S△BOE=24+25
,S△OBC+S△OAB=S△OBF+S△AOF=16
+24,三个式子相加除以2即是三角形ABC的面积.
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
解答: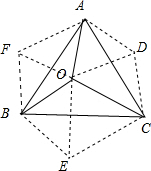 解:将△AOB沿逆时针旋转至△ADC,将△AOC沿逆时针旋转至△BEC,将△BOC沿逆时针旋转至△BFA,
解:将△AOB沿逆时针旋转至△ADC,将△AOC沿逆时针旋转至△BEC,将△BOC沿逆时针旋转至△BFA,
∴OA=AD,∠OAB=∠DAC,OC=EC,∠OCB=∠ECB,
∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,
∴∠OAD=60°,∠OCE=60°,
∴△OAD是等边三角形,
∴OD=OA=6,
∵CD=OB=8,AC=10,
∴OD2+DC2=OC2,
∴△ODC是直角三角形,
∴S△OAD=
OA•
OA=
×6×
×6=9
,S△ODC=
OD•DC=
×6×8=24,
∴S△OAB+S△OAC=S△OAD+,S△ODC=9
+24,
同理可得:S△OCE=
×10×
×10=25
,S△BOE=
×6×8=24,
∴S△OBC+S△OAC=S△OCE+S△BOE=24+25
,
S△OBF=
×8×
×8=16
,S△AOF=
×6×8=24,
∴S△OBC+S△OAB=S△OBF+S△AOF=16
+24,
∴S△ABC=
(9
+24+25
+24+16
+24)=25
+36.
 解:将△AOB沿逆时针旋转至△ADC,将△AOC沿逆时针旋转至△BEC,将△BOC沿逆时针旋转至△BFA,
解:将△AOB沿逆时针旋转至△ADC,将△AOC沿逆时针旋转至△BEC,将△BOC沿逆时针旋转至△BFA,∴OA=AD,∠OAB=∠DAC,OC=EC,∠OCB=∠ECB,
∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,
∴∠OAD=60°,∠OCE=60°,
∴△OAD是等边三角形,
∴OD=OA=6,
∵CD=OB=8,AC=10,
∴OD2+DC2=OC2,
∴△ODC是直角三角形,
∴S△OAD=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△OAB+S△OAC=S△OAD+,S△ODC=9
| 3 |
同理可得:S△OCE=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
∴S△OBC+S△OAC=S△OCE+S△BOE=24+25
| 3 |
S△OBF=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
∴S△OBC+S△OAB=S△OBF+S△AOF=16
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
点评:本题考查了旋转的性质,等边三角形的判定和性质,勾股定理的逆定理的应用,熟练掌握性质定理是关键.

练习册系列答案
相关题目
若在△ABC中,∠C=90°,有一点既在BC的对称轴上,又在AC的对称轴上,则该点一定是( )
| A、C点 | B、BC中点 |
| C、AC中点 | D、AB中点 |
 如图,已知BD=CE=AF,△ABC是正三角形,证明:△DEF是正三角形.
如图,已知BD=CE=AF,△ABC是正三角形,证明:△DEF是正三角形.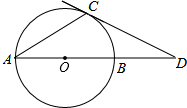 如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠D=30°,求∠A的度数.
如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠D=30°,求∠A的度数.