题目内容
一个直棱柱有14个顶点，所有侧棱长的和为42cm，每条侧棱长为 cm，此棱柱底面形状是 ，若将此棱柱展成平面图形，需剪开 条棱．
考点：几何体的展开图
专题：
分析：根据棱柱的顶点数除以2，是棱柱的棱数，进而可得每条侧棱的长度及此棱柱底面的形状，根据此棱柱的棱的条数以及展开后平面之间应有棱连着，即可得出需剪开的棱的条数．
解答：解：∵一个直棱柱有14个顶点，14÷2=7，
∴此棱柱底面形状是七边形，
∵所有侧棱长的和为42cm，
∴每条侧棱长是42÷7=6（cm），
∵七棱柱有9个表面，21条棱，要展成一个平面图形必须8条棱连接，
∴要剪21-8=13条棱，
故答案为：6，七边形，13．
∴此棱柱底面形状是七边形，
∵所有侧棱长的和为42cm，
∴每条侧棱长是42÷7=6（cm），
∵七棱柱有9个表面，21条棱，要展成一个平面图形必须8条棱连接，
∴要剪21-8=13条棱，
故答案为：6，七边形，13．
点评：此题主要考查了几何体的展开图，规律：n棱柱有（n+2）个面，3n条棱，展成平面图形时，（n+2）个面需有（n+1）条棱相连，故应留下（n+1）条棱不剪，所以要把n棱柱展成平面图形，共需剪3n-（n+1）=（2n-1）条棱．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
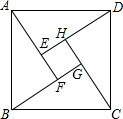四年一度的国际数学家大会于2002年8月20日在北京召开，大会会标如图．它是由四个相同的直角三角形（Rt△AED，Rt△BFA，Rt△CGB，Rt△DHC）与中间的小正方形EFGH拼成的，
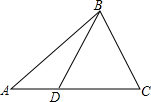已知如图，在△ABC中，D是AC上一点，DC：BC=BC：AC=3：4，△BCD的周长是24cm，求：
如图，P为弦AB上一点，CP⊥OP交⊙O于点C，AB=8，下列判断中正确的是（ ）
| A、四边相等的四边形是正方形 |
| B、四角相等的四边形是矩形 |
| C、对角线互相垂直的平行四边形是正方形 |
| D、对角线互相垂直的四边形是菱形 |