题目内容
如图，已知BD=CE=AF，△ABC是正三角形，证明：△DEF是正三角形．考点：全等三角形的判定与性质,等边三角形的判定与性质
专题：证明题
分析：根据等边△ABC中AD=BE=CF，证得△ADF≌△BEF≌△EFD即可得出△DEF是等边三角形．
解答：证明：∵△ABC是等边三角形，
∴∠A=∠B=∠C=60°，AB=BC=AC，
又∵BD=CE=AF，
∴AD=BE=CF，
在△ADF和△BED中，
，
∴△ADF≌△BED（SAS），
∴DF=DE，
同理，DF=EF，
∴DF=EF=DE．
∴△DEF是等边三角形．
∴∠A=∠B=∠C=60°，AB=BC=AC，
又∵BD=CE=AF，
∴AD=BE=CF，
在△ADF和△BED中，
|
∴△ADF≌△BED（SAS），
∴DF=DE，
同理，DF=EF，
∴DF=EF=DE．
∴△DEF是等边三角形．
点评：本题考查了等边三角形的性质，证得△ADF≌△BEF≌△EFD即可得出△DEF是等边三角形．
练习册系列答案
名校课堂系列答案
相关题目
一斜坡坡角约为30°，经测量坡顶铅垂高度为30米，则坡面的长约为（ ）米．
| A、90米 | ||
| B、60米 | ||
| C、20 | ||
D、30
|
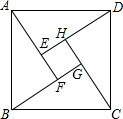四年一度的国际数学家大会于2002年8月20日在北京召开，大会会标如图．它是由四个相同的直角三角形（Rt△AED，Rt△BFA，Rt△CGB，Rt△DHC）与中间的小正方形EFGH拼成的，