题目内容
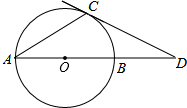 如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠D=30°,求∠A的度数.
如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠D=30°,求∠A的度数.考点:切线的性质
专题:计算题
分析:连结OC,如图,根据切线的性质得∠OCD=90°,再利用互余得∠COD=60°,由于OA=OC,则∠A=∠ACO,然后根据三角形外角性质求解.
解答: 解:连结OC,如图,
解:连结OC,如图,
∵CD为⊙O的切线,
∴OC⊥CD,
∴∠OCD=90°,
而∠D=30°,
∴∠COD=60°,
∵OA=OC,
∴∠A=∠ACO,
∴∠COD=∠A+∠ACO=2∠A,
∴∠A=
×60°=30°.
 解:连结OC,如图,
解:连结OC,如图,∵CD为⊙O的切线,
∴OC⊥CD,
∴∠OCD=90°,
而∠D=30°,
∴∠COD=60°,
∵OA=OC,
∴∠A=∠ACO,
∴∠COD=∠A+∠ACO=2∠A,
∴∠A=
| 1 |
| 2 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了等腰三角形的性质.

练习册系列答案
相关题目
下列判断中正确的是( )
| A、四边相等的四边形是正方形 |
| B、四角相等的四边形是矩形 |
| C、对角线互相垂直的平行四边形是正方形 |
| D、对角线互相垂直的四边形是菱形 |
 如图,P为弦AB上一点,CP⊥OP交⊙O于点C,AB=8,
如图,P为弦AB上一点,CP⊥OP交⊙O于点C,AB=8, 如图,AB为⊙O的直径,C为半圆的中点,⊙C的半径为2,AB=8,点P是直径AB上的一动点,PM与⊙C切于点M,则PM的取值范围为
如图,AB为⊙O的直径,C为半圆的中点,⊙C的半径为2,AB=8,点P是直径AB上的一动点,PM与⊙C切于点M,则PM的取值范围为