题目内容
10.解下列不等式,并在数轴上表示解集:(1)$\frac{3}{2}$x-1≤2x;
(2)4(x-1)+3>3x.
分析 (1)移项、合并同类项、系数化为1后可得解集,根据大于向右,包括用实心点在数轴上表示解集即可;
(2)去括号后移项、合并同类项可得不等式解集,根据大于向右,不包括改数用空心点在数轴上表示解集即可.
解答 解:(1)移项,得:$\frac{3}{2}$x-2x≤1,
合并同类项,得:-$\frac{1}{2}$x≤1,
系数化为1,得:x≥-2,
在数轴上表示解集如下:
(2)去括号,得:4x-4+3>3x,
移项、合并,得:x>1,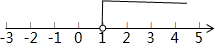 .
.
点评 本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.

练习册系列答案
相关题目
20.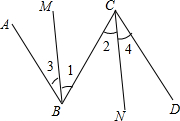 如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )
如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )
 如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )
如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )| A. | ∠1=∠2 | B. | ∠1=∠3且∠2=∠4 | ||
| C. | BM∥CN | D. | ∠1与∠2互补且不相等 |
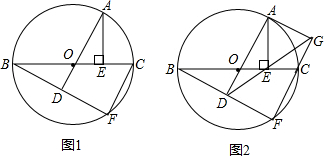
 在?ABCD中,已知∠A=25°,将△BDA沿BD翻折至△BDA′,连接CA′,∠DA′C=55°,则∠ABD=30°.
在?ABCD中,已知∠A=25°,将△BDA沿BD翻折至△BDA′,连接CA′,∠DA′C=55°,则∠ABD=30°.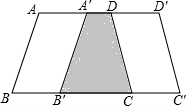 如图,在梯形ABCD中,AD∥BC,AD=4cm,BC=6cm.梯形ABCD的高为5cm、试问将梯形ABCD沿着AD方向平移多少厘米才能使平移后的梯形与原来的梯形ABCD重叠部分的面积为10cm2?
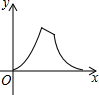
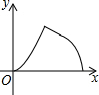
如图,在梯形ABCD中,AD∥BC,AD=4cm,BC=6cm.梯形ABCD的高为5cm、试问将梯形ABCD沿着AD方向平移多少厘米才能使平移后的梯形与原来的梯形ABCD重叠部分的面积为10cm2?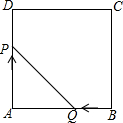 如图,边长为3的正方形ABCD,点P从点A出发以每秒3个单位长度的速度沿A→D→C→B运动,点Q从点B出发以每秒1个单位长度的速度向点A运动,当一个点到达终点时,另一个点也随之停止运动.设△APQ的面积为y,运动时间为x秒,则能大致反映y与x的函败关系的图象是( )
如图,边长为3的正方形ABCD,点P从点A出发以每秒3个单位长度的速度沿A→D→C→B运动,点Q从点B出发以每秒1个单位长度的速度向点A运动,当一个点到达终点时,另一个点也随之停止运动.设△APQ的面积为y,运动时间为x秒,则能大致反映y与x的函败关系的图象是( )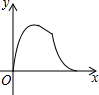

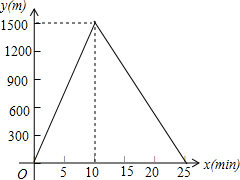 小明从家到达A地后立即返回,他离家的路程y(m)与所用时间x(min)的函数图象如图所示,小明去时路过报亭C与返回时路过报亭C相隔10min.
小明从家到达A地后立即返回,他离家的路程y(m)与所用时间x(min)的函数图象如图所示,小明去时路过报亭C与返回时路过报亭C相隔10min.