Question

12．如图，在四边形ABCD中，AC=BD=6，E、F、G、H分别是AB、BC、CD、DA的中点，则EG²+FH²的值为（　　）

• A． 9
• B． 18
• C． 36
• D． 48

Answer 1

分析 作辅助线，构建四边形EFGH，证明它是菱形，利用对角线互相垂直和勾股定理列等式，再利用中位线性质等量代换可得结论．

解答 解：连接EF、FG、GH、EH，
∵E、F、G、H分别是AB、BC、CD、DA的中点，
∴EF∥AC，HG∥AC，EF=$\frac{1}{2}$AC，FG=$\frac{1}{2}$BD，
∴EF∥HG，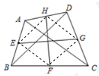
同理EH∥FG，
∴四边形EFGH为平行四边形，
∵AC=BD，
∴EF=FG，
∴平行四边形EFGH为菱形，
∴EG⊥FH，EG=2OG，FH=2OH，
∴EG²+FH²=（2OE）²+（2OH）²=4（OE²+OH²）=4EH²=4×（$\frac{1}{2}$BD）²=6²=36；
故选C．

点评 本题考查了中点四边形，运用了三角形中位线的性质，将三角形和四边形有机结合，把边的关系由三角形转化为四边形中，可以证明四边形为特殊的四边形；对于线段的平方和可以利用勾股定理来证明．