题目内容
14.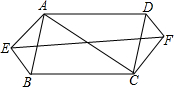 如图,已知AB∥DC,∠ABC=∠ADC,AE=CF,BE=DF,求证:EF与AC互相平分.
如图,已知AB∥DC,∠ABC=∠ADC,AE=CF,BE=DF,求证:EF与AC互相平分.
分析 连接AF、CE,由平行线的性质得出∠ABC+∠BCD=180°,∠BAC=∠DCA,证出∠ADC+∠BCD=180°,得出AD∥BC,证出四边形ABCD是平行四边形,得出AB=CD,由SSS证明△ABE≌△CDF,得出AE=CF,证出AE∥CF,得出四边形AECF是平行四边形,即可得出结论.
解答 证明:连接AF、CE,如图所示: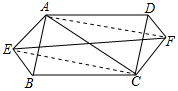
∵AB∥DC,
∴∠ABC+∠BCD=180°,∠BAC=∠DCA,
∵∠ABC=∠ADC,
∴∠ADC+∠BCD=180°,
∴AD∥BC,
∴四边形ABCD是平行四边形,
∴AB=CD,
在△ABE和△CDF中,$\left\{\begin{array}{l}{AE=CF}&{\;}\\{BE=DF}&{\;}\\{AB=CD}&{\;}\end{array}\right.$,
∴△ABE≌△CDF(SSS),
∴AE=CF,∠BAE=∠DCF,
∴∠EAC=∠FCA,
∴AE∥CF,
∴四边形AECF是平行四边形,
∴EF与AC互相平分.
点评 本题考查了平行四边形的判定与性质、全等三角形的判定与性质;熟练掌握平行四边形的性质与性质,证明三角形全等是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.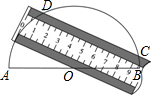 如图,将一个一边有刻度的直尺放在一个量角器上,使其一边经过量角器的圆心O另一边与量角器交于C、D两点,且C、D两点在直尺上的刻度分别为2、10在量角器上的刻度分别为50、170,则直尺的宽为( )
如图,将一个一边有刻度的直尺放在一个量角器上,使其一边经过量角器的圆心O另一边与量角器交于C、D两点,且C、D两点在直尺上的刻度分别为2、10在量角器上的刻度分别为50、170,则直尺的宽为( )
 如图,将一个一边有刻度的直尺放在一个量角器上,使其一边经过量角器的圆心O另一边与量角器交于C、D两点,且C、D两点在直尺上的刻度分别为2、10在量角器上的刻度分别为50、170,则直尺的宽为( )
如图,将一个一边有刻度的直尺放在一个量角器上,使其一边经过量角器的圆心O另一边与量角器交于C、D两点,且C、D两点在直尺上的刻度分别为2、10在量角器上的刻度分别为50、170,则直尺的宽为( )| A. | 2 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
 如图,矩形城ABCD,东边城墙AB=6km,南边城墙AD=4km,东门点E、南门点F分别是AB、AD的中点,EG⊥AB,FH⊥AD,EG=8km,HG经过A点,求FH的长.
如图,矩形城ABCD,东边城墙AB=6km,南边城墙AD=4km,东门点E、南门点F分别是AB、AD的中点,EG⊥AB,FH⊥AD,EG=8km,HG经过A点,求FH的长. 如图在△ABC和△DEF中,∠B=50°,∠A=41°,∠E=50°,∠F=89°,求证:△ABC∽△DEF.
如图在△ABC和△DEF中,∠B=50°,∠A=41°,∠E=50°,∠F=89°,求证:△ABC∽△DEF.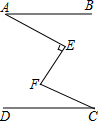 已知AB∥CD,∠AEF=90°,∠EFC=60°,探究∠A与∠C的数量关系并说明道理.
已知AB∥CD,∠AEF=90°,∠EFC=60°,探究∠A与∠C的数量关系并说明道理. 小颖想测量教学楼前的一棵树AB的高度,课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,如图:她先测得留在墙壁上的影高CD为1.2m,又测得地面的影长BD为2.4m,请你帮她算一下,树高是多少?
小颖想测量教学楼前的一棵树AB的高度,课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,如图:她先测得留在墙壁上的影高CD为1.2m,又测得地面的影长BD为2.4m,请你帮她算一下,树高是多少?