题目内容
20.计算:$\frac{2a}{a+1}$÷(a-1)+$\frac{{a}^{2}-1}{{a}^{2}+2a+1}$.分析 结合分式混合运算的运算法则进行求解即可.
解答 解:原式=$\frac{2a}{a+1}$×$\frac{1}{a-1}$+$\frac{(a-1)(a+1)}{(a+1)^{2}}$
=$\frac{2a}{(a+1)(a-1)}$+$\frac{a-1}{a+1}$
=$\frac{2a}{(a+1)(a-1)}$+$\frac{(a-1)^{2}}{(a+1)(a-1)}$
=$\frac{{a}^{2}+1}{{a}^{2}-1}$.
点评 本题考查了分式的混合运算,解答本题的关键在于熟练掌握分式混合运算的运算法则.

练习册系列答案
相关题目
11. 如图,在?ABCD中,点E是边BA延长线上的一点,CE交AD于点F.下列各式中,错误的是( )
如图,在?ABCD中,点E是边BA延长线上的一点,CE交AD于点F.下列各式中,错误的是( )
 如图,在?ABCD中,点E是边BA延长线上的一点,CE交AD于点F.下列各式中,错误的是( )
如图,在?ABCD中,点E是边BA延长线上的一点,CE交AD于点F.下列各式中,错误的是( )| A. | $\frac{AE}{AB}=\frac{FE}{FC}$ | B. | $\frac{AE}{AB}=\frac{AF}{DF}$ | C. | $\frac{AE}{AB}=\frac{AF}{BC}$ | D. | $\frac{AE}{BE}=\frac{AF}{BC}$ |
5.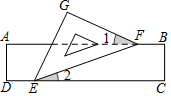 如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=22°,那么∠2的度数是( )
如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=22°,那么∠2的度数是( )
 如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=22°,那么∠2的度数是( )
如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=22°,那么∠2的度数是( )| A. | 30° | B. | 23° | C. | 20° | D. | 15° |
 如图,边长为x的正方形中有两个半圆形
如图,边长为x的正方形中有两个半圆形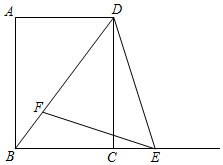 如图,已知四边形ABCD是矩形,cot∠ADB=$\frac{3}{4}$,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.
如图,已知四边形ABCD是矩形,cot∠ADB=$\frac{3}{4}$,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB. 如图所示的几何体是由五个完全相同的正方体组成的,与这个几何体的主视图不相同的是( )
如图所示的几何体是由五个完全相同的正方体组成的,与这个几何体的主视图不相同的是( )


