题目内容
4.从-3,-2,-1,1,2,3六个数中任选一个数记为k,则使得关于x的分式方程$\frac{k-1}{x+1}$=k-2有解,且关于x的一次函数y=(k+$\frac{3}{2}$)x+2不经过第四象限的概率为$\frac{1}{3}$.分析 首先利用分式方程的知识求得当k=-3,-2,-1,3,使得关于x的分式方程$\frac{k-1}{x+1}$=k-2有解,再利用一次函数的性质,求得当k=-1,1,2,3时,关于x的一次函数y=(k+$\frac{3}{2}$)x+2不经过第四象限,再利用概率公式即可求得答案.
解答 解:∵方程两边同乘以(x+1),
∴k-1=(k-2)(x+1),
∴当k=2或k=1时,关于x的分式方程$\frac{k-1}{x+1}$=k-2无解,
∴当k=-3,-2,-1,3,使得关于x的分式方程$\frac{k-1}{x+1}$=k-2有解;
∵关于x的一次函数y=(k+$\frac{3}{2}$)x+2不经过第四象限,
∴k+$\frac{3}{2}$>0,
∴k>-$\frac{3}{2}$,
∴当k=-1,1,2,3时,关于x的一次函数y=(k+$\frac{3}{2}$)x+2不经过第四象限,
∴得关于x的分式方程$\frac{k-1}{x+1}$=k-2有解,且关于x的一次函数y=(k+$\frac{3}{2}$)x+2不经过第四象限的有-1,3;
∴使得关于x的分式方程$\frac{k-1}{x+1}$=k-2有解,且关于x的一次函数y=(k+$\frac{3}{2}$)x+2不经过第四象限的概率为:$\frac{2}{6}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 此题考查了概率公式的应用、一次函数的性质以及分式方程.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
14. 如图,小明家相对于学校的位置,下列描述最正确的是( )
如图,小明家相对于学校的位置,下列描述最正确的是( )
 如图,小明家相对于学校的位置,下列描述最正确的是( )
如图,小明家相对于学校的位置,下列描述最正确的是( )| A. | 在距离学校300米处 | B. | 在学校的西北方向 | ||
| C. | 在西北方向300米处 | D. | 在学校西北方向300米处 |
12.$\sqrt{\frac{1}{16}}$的平方根是( )
| A. | ±$\frac{1}{2}$ | B. | ±$\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
19.如果m=$\sqrt{10}$-1,那么m的取值范围是( )
| A. | 0<m<1 | B. | 1<m<2 | C. | 2<m<3 | D. | 3<m<4 |
9.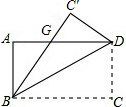 如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.则△BDG的面积的值是( )
如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.则△BDG的面积的值是( )
 如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.则△BDG的面积的值是( )
如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.则△BDG的面积的值是( )| A. | 18.75cm2 | B. | 19.15cm2 | C. | 20cm2 | D. | 21.35cm2 |
13.下列运算正确的是( )
| A. | 2$\sqrt{2}×\sqrt{2}=4$ | B. | 2a3•a4=2a7 | C. | (2a4)3=8a7 | D. | a8÷a2=a4 |
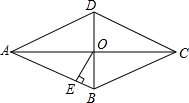 如图,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E,若∠BAD:∠ADC=1:4,则∠AOE的大小为72°.
如图,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E,若∠BAD:∠ADC=1:4,则∠AOE的大小为72°.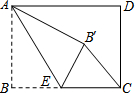 如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,把∠B沿AE折叠,使点B落在点B′处,则:①AB′=3;②当△CEB′为直角三角形时,BE=3或$\frac{3}{2}$.
如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,把∠B沿AE折叠,使点B落在点B′处,则:①AB′=3;②当△CEB′为直角三角形时,BE=3或$\frac{3}{2}$.