题目内容
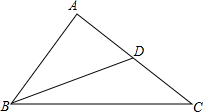 如图,AB=4,BC=6,BD为△ABC的中线,求BD的范围.
如图,AB=4,BC=6,BD为△ABC的中线,求BD的范围.考点:全等三角形的判定与性质,三角形三边关系
专题:
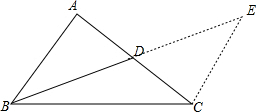
分析:延长BD到E使DE=DB,连结CE,就可以得出△ADB≌CDE,就可以得出AB=CE,就有BC-CE<BE<BC+CE,就可以求出结论.
解答:解:延长BD到E使DE=DB,连结CE,
∵BD为△ABC的中线,
∴AD=CD.
在△ADB和CDE中,
,
∴△ADB≌CDE(SAS),
∴AB=CE.
∵BC-CE<BE<BC+CE,
∴BC-AB<2BD<BC+AB.
∵AB=4,BC=6,
∴2<2BD<10,
∴1<BD<5.
答:BD的范围为:1<BD<5.
∵BD为△ABC的中线,
∴AD=CD.
在△ADB和CDE中,
|

∴△ADB≌CDE(SAS),
∴AB=CE.
∵BC-CE<BE<BC+CE,
∴BC-AB<2BD<BC+AB.
∵AB=4,BC=6,
∴2<2BD<10,
∴1<BD<5.
答:BD的范围为:1<BD<5.
点评:本题考查了三角形的中线的运用,全等三角形的判定及性质的运用,三角形三边关系的运用,解答时证明三角形全等是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如果方程5x-1=□x+3的解得x=-2,则□是( )
| A、4 | B、7 | C、-7 | D、-14 |
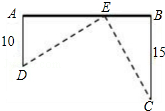 如图,在笔直的铁路上A、B两点相距25km,C、D为两村庄,DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等.则E应建在距A
如图,在笔直的铁路上A、B两点相距25km,C、D为两村庄,DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等.则E应建在距A 如图,在矩形ABCD中,AB=9,AD=3
如图,在矩形ABCD中,AB=9,AD=3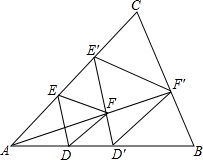 等边三角形的三个顶点分别在一个三角形的三条边上,我们称这个三角形为这个三角形的“内接等边三角形”,
等边三角形的三个顶点分别在一个三角形的三条边上,我们称这个三角形为这个三角形的“内接等边三角形”,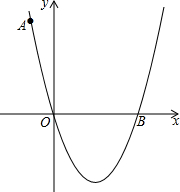 如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过O(0,0),A(-1,5),B(4,0)三点,请在该抛物线对称轴上作一点P,使得AP+OP的值最小,并求出最小值.(请用尺规作图完成,不写作法,但保留作图痕迹)
如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过O(0,0),A(-1,5),B(4,0)三点,请在该抛物线对称轴上作一点P,使得AP+OP的值最小,并求出最小值.(请用尺规作图完成,不写作法,但保留作图痕迹)