题目内容
11．四条线段a，b，c，d成比例，其中a=3cm，d=4cm，c=6cm，则b等于（ ）| A． | 8cm | B． | 4.5cm | C． | 1.5cm | D． | 2cm |
分析 根据成比例线段的概念，得a：b=c：d，再根据比例的基本性质，求得b的值．
解答 解：∵四条线段a、b、c、d成比例，
∴$\frac{a}{b}$=$\frac{c}{d}$，
∵a=3cm，d=4cm，c=6cm，
∴$\frac{3}{b}$=$\frac{6}{4}$，
解得：b=2cm．
故选D．
点评 此题考查了比例线段，理解比例线段的概念，写比比例式是本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
2．
如图，⊙O是△ABC的外接圆，连接OA、OB，∠AOB=50°，则∠C的度数为（ ）
如图，⊙O是△ABC的外接圆，连接OA、OB，∠AOB=50°，则∠C的度数为（ ）| A． | 25° | B． | 40° | C． | 50° | D． | 80° |
如图，∠AOB=42°，∠BOC=86°，OD为∠AOC的平分线，∠BOD=22°．
6．
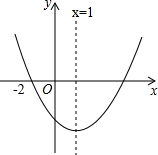二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论中：①abc＜0；②2a+b=0；③当-2＜x＜3，y＜0；④当x＞1时，y随x的增大而减小，正确的个数是（ ）
二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论中：①abc＜0；②2a+b=0；③当-2＜x＜3，y＜0；④当x＞1时，y随x的增大而减小，正确的个数是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
已知，正六边形ABCDEF在直角坐标系的位置如图所示，A（-2，0），点B在原点，把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转，每次翻转60°，经过5次翻转之后，点B的坐标是（11，$\sqrt{3}$）．
在直角坐标系中，过一点分别作坐标轴的垂线，若与坐标轴围成矩形的周长与面积相等，则这个点叫做和谐点．例如，图中过点P分别作x轴，y轴的垂线，与坐标轴围成矩形OAPB的周长与面积相等，则点P是和谐点．
1．已知二次函数y=ax2+bx+c（a≠0，a，b，c为常数）的y与x的部分对应值如下表：
判断方程ax2+bx+c=0的一个解x的取值范围是（ ）
| x | 3.23 | 3.24 | 3.25 | 3.26 |
| y | -0.06 | -0.08 | -0.03 | 0.09 |
| A． | 3＜x＜3.23 | B． | 3.23＜x＜3.24 | C． | 3.24＜x＜3.25 | D． | 3.25＜x＜3.26 |