题目内容
19. 如图,∠AOB=42°,∠BOC=86°,OD为∠AOC的平分线,∠BOD=22°.
如图,∠AOB=42°,∠BOC=86°,OD为∠AOC的平分线,∠BOD=22°.
分析 首先求得∠AOC的度数,根据角平分线的定义求得∠AOD,然后根据∠BOD=∠AOD-∠AOB求解.
解答 解:∵∠AOB=42°,∠BOC=86°,
∴∠AOC=∠AOB+∠BOC=42°+86°=128゜,
∵OD平分∠AOC,
∴∠AOD=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×128°=64°,
∴∠BOD=∠AOD-∠AOB=64゜-42゜=22°.
故答案为:22゜.
点评 本题考查了角度的计算,正确理解角平分线的定义,求得∠AOD是关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
14. 如图:已知⊙P的半径为1,圆心P在抛物线y=$\frac{1}{2}{x}^{2}-1$上运动,当⊙P与x轴相切时,圆心P的坐标为( )
如图:已知⊙P的半径为1,圆心P在抛物线y=$\frac{1}{2}{x}^{2}-1$上运动,当⊙P与x轴相切时,圆心P的坐标为( )
 如图:已知⊙P的半径为1,圆心P在抛物线y=$\frac{1}{2}{x}^{2}-1$上运动,当⊙P与x轴相切时,圆心P的坐标为( )
如图:已知⊙P的半径为1,圆心P在抛物线y=$\frac{1}{2}{x}^{2}-1$上运动,当⊙P与x轴相切时,圆心P的坐标为( )| A. | (-2,1) | B. | (2,1) | C. | (0,-1) | D. | (-2,1)或(2,1)或(0,-1) |
11.四条线段a,b,c,d成比例,其中a=3cm,d=4cm,c=6cm,则b等于( )
| A. | 8cm | B. | 4.5cm | C. | 1.5cm | D. | 2cm |


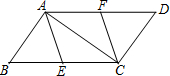 已知,如图,在?ABCD中,AC是对角线,AB=AC,点E、F分别是BC、AD的中点,连接AE,CF.
已知,如图,在?ABCD中,AC是对角线,AB=AC,点E、F分别是BC、AD的中点,连接AE,CF. 为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5m.按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,请你根据该图计算CD,CE的长,并标明限制高度.
为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5m.按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,请你根据该图计算CD,CE的长,并标明限制高度. 如图,水平放置的容器内原有210毫米高的水,将若干个球逐一放入该容器中个,毎放入1个大球水面上升4毫米,每放入一个小球水面就上升若干毫米,假定放入容器中的所有球完全浸没水中且水不溢出.
如图,水平放置的容器内原有210毫米高的水,将若干个球逐一放入该容器中个,毎放入1个大球水面上升4毫米,每放入一个小球水面就上升若干毫米,假定放入容器中的所有球完全浸没水中且水不溢出.