题目内容
2.从-2,-1,0,1这四个数中任取两个不同的数作为一次函数y=kx+b的一次项系数k和常数项b.那么一次函数y=kx+b图象不经过第三象限的概率为$\frac{5}{12}$.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所得一次函数y=kx+b的图象不经过第三象限的情况,再利用概率公式求解即可求得答案.
解答 解:列表得:
| (-2,1) | (-1,1) | (0,1) | -- |
| (-2,0) | (-1,0) | -- | (1,0) |
| (-2,-1) | -- | (0,-1) | (1,-1) |
| -- | (-1,-2) | (0,-2) | (1,-2) |
∵使得一次函数y=kx+b图象不经过第三象限的有(0,1),(-2,0),(-2,1),(-1,0),(-1,1),
∴使得一次函数y=kx+b图象不经过第三象限的概率为$\frac{5}{12}$.
故答案为:$\frac{5}{12}$.
点评 此题考查了用列表法或树状图法求概率与一次函数的性质.解此题的关键是准确列表或画树形图,找出所有的可能情况,即可求得概率.

练习册系列答案
相关题目
13.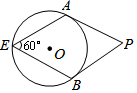 如图,PA、PB是⊙O的切线,切点分别是A、B,如果∠E=60°,那么∠P等于( )
如图,PA、PB是⊙O的切线,切点分别是A、B,如果∠E=60°,那么∠P等于( )
 如图,PA、PB是⊙O的切线,切点分别是A、B,如果∠E=60°,那么∠P等于( )
如图,PA、PB是⊙O的切线,切点分别是A、B,如果∠E=60°,那么∠P等于( )| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
17. 如图中主三视图对应的三棱柱是( )
如图中主三视图对应的三棱柱是( )
 如图中主三视图对应的三棱柱是( )
如图中主三视图对应的三棱柱是( )| A. |  | B. |  | C. |  | D. |  |
11.下列条件能判定△ABC为等腰三角形的是( )
| A. | ∠A=30°,∠B=60° | B. | AB=5,AC=12,BC=13 | ||
| C. | ∠A=50°,∠B=80° | D. | ∠A:∠B:∠C=3:4:5 |
12.下列计算正确的是( )
| A. | a2•a3=a6 | B. | (a2)3=a5 | C. | (-2ab)2=4a2b2 | D. | 3a2b2÷a2b2=3ab |
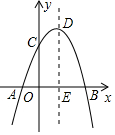 如图,在平面直角坐标系xOy中,抛物线与x轴交于点A(-1,0),B(3,0),与y轴交于点C(0,3),抛物线的顶点为D,对称轴与x轴交于点E.
如图,在平面直角坐标系xOy中,抛物线与x轴交于点A(-1,0),B(3,0),与y轴交于点C(0,3),抛物线的顶点为D,对称轴与x轴交于点E.