题目内容
7.计算或化简(1)$\sqrt{8}$+|-2|-4sin45°-($\frac{1}{3}$)-1
(2)解方程$\frac{2x+2}{x}$-$\frac{x+2}{x-2}$=$\frac{{x}^{2}-2}{{x}^{2}-2x}$.
分析 (1)原式利用二次根式性质,绝对值的代数意义,特殊角的三角函数值,以及负整数指数幂法则计算即可得到结果;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=2$\sqrt{2}$+2-2$\sqrt{2}$-3=-1;
(2)去分母得:2x2-2x-4-x2-2x=x2-2,
解得:x=-$\frac{1}{2}$,
经检验x=-$\frac{1}{2}$是分式方程的解.
点评 此题考查了解分式方程,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
18.下列各式由左边到右边的变形中,是分解因式的为( )
| A. | a (x+y)=a x+a y | B. | x2-4x+4=x(x-4)+4 | ||
| C. | 10x2-5x=5x(2x-1) | D. | x2-16+3x=(x-4)(x+4)+3x |
16.不等式ax+b>0(a<0)的解集是( )
| A. | x>-$\frac{b}{a}$ | B. | x<-$\frac{b}{a}$ | C. | x>$\frac{b}{a}$ | D. | x<$\frac{b}{a}$ |
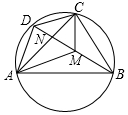 已知圆内接四边形ABCD的对角线AC、BD交于N点,M在BD上,且∠DAN=∠BAM,∠DCN=∠BCM.求证:
已知圆内接四边形ABCD的对角线AC、BD交于N点,M在BD上,且∠DAN=∠BAM,∠DCN=∠BCM.求证: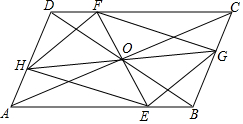 如图所示,过?ABCD的对角线交点O作直线EF,GH分别交各边于点E,F,G,H,依次连接E,G,F,H.求证:四边形EGFH是平行四边形.
如图所示,过?ABCD的对角线交点O作直线EF,GH分别交各边于点E,F,G,H,依次连接E,G,F,H.求证:四边形EGFH是平行四边形. 如图,将周长为4的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为( )
如图,将周长为4的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为( )