题目内容
17．已知一个正多边形相邻的内角比外角大140°．（1）求这个正多边形的内角与外角的度数；
（2）直接写出这个正多边形的边数；
（3）只用这个正多边形若干个，能否镶嵌？并说明理由．
分析 （1）可根据正多边形的一个内角与外角互补可得外角的度数，内角的度数；
（2）360°除以一个外角的度数即为多边形的边数；
（3）一种正多边形的镶嵌应符合一个内角度数能整除360°．
解答 解：（1）设正多边形的外角为x°，则内角为（180-x）°，
∴180-x-x=140，
解得x=20，
∴正多边形的内角为160°，外角为20°；
（2）这个正多边形的边数为：360°÷20°=18．
（3）正多边形的内角为160°，不能整除360°，不能镶嵌．
点评 本题主要考查多边形内角和与外角和，解题的关键是多边形的内角和与外角和以及一种正多边形的镶嵌应符合一个内角度数能整除360°．
练习册系列答案
相关题目
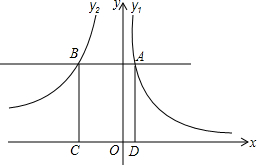如图，反比例函数y1=$\frac{2}{x}$（x＞0）与y2=$\frac{-6}{x}$（x＜0），点A是y1上一动点，过点A作x轴的平行线交y轴于点B，过点A、B作x轴的垂线，垂足为D、C．
2．下列方程是二元一次方程的是（ ）
| A． | 2x+y=3z | B． | 2x-$\frac{1}{y}$=2 | C． | 2xy-3y=0 | D． | 3x-5y=2 |