题目内容
7.计算:$\frac{1}{2+tan60°}$-|cos45°-1|+(-2015)0+3${\;}^{\frac{1}{2}}$.分析 根据零指数幂、分数指数幂和特殊角的三角函数值得到原式=$\frac{1}{2+\sqrt{3}}$-|$\frac{\sqrt{2}}{2}$-1|+1+$\sqrt{3}$,然后分母有理化和去绝对值后合并即可.
解答 解:原式=$\frac{1}{2+\sqrt{3}}$-|$\frac{\sqrt{2}}{2}$-1|+1+$\sqrt{3}$
=2-$\sqrt{3}$+$\frac{\sqrt{2}}{2}$-1+1+$\sqrt{3}$
=2+$\frac{\sqrt{2}}{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂和分数指数幂.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
15.下列属于最简二次根式的是( )
| A. | $\sqrt{{a}^{2}+{b}^{2}}$ | B. | $\sqrt{\frac{1}{b}}$ | C. | $\sqrt{0.1}$ | D. | $\sqrt{18}$ |
12. 如图,一个几何体是由六个大小相同,棱长为1的立方块组成,则从上面看到的图形的面积是( )
如图,一个几何体是由六个大小相同,棱长为1的立方块组成,则从上面看到的图形的面积是( )
 如图,一个几何体是由六个大小相同,棱长为1的立方块组成,则从上面看到的图形的面积是( )
如图,一个几何体是由六个大小相同,棱长为1的立方块组成,则从上面看到的图形的面积是( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
16.若4个数6,x,8,10的中位数为7,则x的取值范围是( )
| A. | x=6 | B. | x=7 | C. | x≤6 | D. | x≥8 |
 如图,四边形ABCD的对角线AC和BD的长分别为4cm和6m,点E、F、G、H分别是AB,BC,CD,AD的中点,求四边形EFGH的周长.
如图,四边形ABCD的对角线AC和BD的长分别为4cm和6m,点E、F、G、H分别是AB,BC,CD,AD的中点,求四边形EFGH的周长. 某班主任把本班学生上学方式的调查结果绘制成如图所示的不完整的统计图,已知骑自行车上学的学生有26人,则采用其他方式上学的学生人数为4 人.
某班主任把本班学生上学方式的调查结果绘制成如图所示的不完整的统计图,已知骑自行车上学的学生有26人,则采用其他方式上学的学生人数为4 人.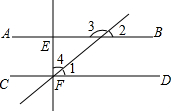 如图,AB∥CD,∠3:∠2=3:2,EF⊥CD,求∠4的度数.
如图,AB∥CD,∠3:∠2=3:2,EF⊥CD,求∠4的度数.