题目内容
6.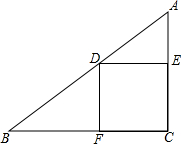 如图所示,D是Rt△ABC斜边上的一点,DE⊥AC,DF⊥BC,垂足分别为E,F,且DE=DF.若AD=3,DB=4,试求S△ADE+S△BDF的值.
如图所示,D是Rt△ABC斜边上的一点,DE⊥AC,DF⊥BC,垂足分别为E,F,且DE=DF.若AD=3,DB=4,试求S△ADE+S△BDF的值.
分析 连接CD,由DE⊥AC、DF⊥BC、∠ECF=90°、DE=DF可得出四边形AFCE为正方形,根据正方形的性质可知CD平分∠ACB,根据角平分线的性质可得出$\frac{AD}{AC}$=$\frac{DB}{BC}$,设AC=3x,则BC=4x,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5x.根据AB=7可求出x值,进而得出AC、BC的值,再根据相似三角形的性质可得出S△ADE、S△BDF与S△ABC之间的关系,结合三角形的面积公式即可求出S△ADE+S△BDF的值.
解答 解:连接CD,如图所示.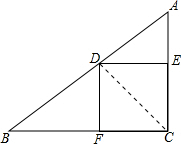
∵DE⊥AC,DF⊥BC,∠ECF=90°,DE=DF,
∴四边形AFCE为正方形,
∴CD平分∠ACB,
∴$\frac{AD}{AC}$=$\frac{DB}{BC}$.
∵AD=3,DB=4,
∴设AC=3x,则BC=4x,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5x.
∵AB=AD+DB=7,
∴x=$\frac{7}{5}$,
∴AC=$\frac{21}{5}$,BC=$\frac{28}{5}$.
∵∠A=∠A,∠AED=∠ACB=90°,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{AD}{AB}$)2=$\frac{9}{49}$.
同理可得:$\frac{{S}_{△BDF}}{{S}_{△BAC}}$=($\frac{DB}{AB}$)2=$\frac{16}{49}$.
∵S△ABC=$\frac{1}{2}$AC•BC=$\frac{294}{25}$,
∴S△ADE+S△BDF=($\frac{9}{49}$+$\frac{16}{49}$)S△ABC=6.
点评 本题考查了角平分线的性质、正方形的判定与性质、相似三角形的判定与性质以及三角形的面积,根据相似三角形的性质找出S△ADE、S△BDF与S△ABC之间的关系是解题的关键.

| A. | $\sqrt{2}$+1 | B. | -$\sqrt{2}$+1 | C. | -$\sqrt{2}$-1 | D. | $\sqrt{2}$-1 |
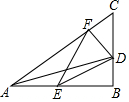 如图,△ABC中,∠B=90°,∠C=60°,AD平分∠BAC交BC于D,过D作DF⊥AC于F,E在AB上,且DE=AE,连结EF.若AB=4+2$\sqrt{3}$,则EF的长为( )
如图,△ABC中,∠B=90°,∠C=60°,AD平分∠BAC交BC于D,过D作DF⊥AC于F,E在AB上,且DE=AE,连结EF.若AB=4+2$\sqrt{3}$,则EF的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$ |
 如图,在平面直角坐标系中,以原点O为圆心的同心圆的半径由内向外依次为1,2,3,4,…,同心圆与直线y=x和y=-x分别交于A1,A2,A3,A4,…,则A30的坐标是( )
如图,在平面直角坐标系中,以原点O为圆心的同心圆的半径由内向外依次为1,2,3,4,…,同心圆与直线y=x和y=-x分别交于A1,A2,A3,A4,…,则A30的坐标是( )| A. | (4$\sqrt{2}$,-4$\sqrt{2}$) | B. | (-4$\sqrt{2}$,4$\sqrt{2}$) | C. | (-8$\sqrt{2}$,8$\sqrt{2}$) | D. | (30,30) |
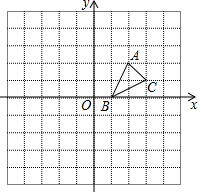 如图,△ABC的顶点的坐标分别为A(2,2),B(1,0),C(3,1).
如图,△ABC的顶点的坐标分别为A(2,2),B(1,0),C(3,1). 在长方体ABCD-EFGH中,与平面ABCD和平面ABFE都平行的棱是GH.
在长方体ABCD-EFGH中,与平面ABCD和平面ABFE都平行的棱是GH. 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A﹙-2,-5﹚,C﹙5,n),交y轴于点B,交x轴于点D.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A﹙-2,-5﹚,C﹙5,n),交y轴于点B,交x轴于点D.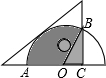 将一块三角板和半圆形量角器按图中方式叠放,重叠部分(阴影)的量角器的圆弧AB对应的圆心角∠AOB=120°,OC=2cm,则图中阴影部分的面积为($\frac{16π}{3}$+2$\sqrt{3}$)cm2.
将一块三角板和半圆形量角器按图中方式叠放,重叠部分(阴影)的量角器的圆弧AB对应的圆心角∠AOB=120°,OC=2cm,则图中阴影部分的面积为($\frac{16π}{3}$+2$\sqrt{3}$)cm2.