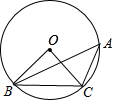如图.点A.B.C在⊙O上.若∠BAC=45°.OB=2.则BC的长为( )A．2B．4C．$\sqrt{2}$D．2$\sqrt{2}$ 题目和参考答案——青夏教育精英家教网—

题目内容

15．

如图，点A、B、C在⊙O上，若∠BAC=45°，OB=2，则BC的长为（　　）

A．

B．

C．

$\sqrt{2}$

D．

2$\sqrt{2}$

分析利用圆周角定理可以推知∠BOC=90°，然后在直角△BOC中，利用勾股定理来求BC的长度．

解答解：如图，∵∠BAC=45°，
∴∠BOC=90°，
∵OB=OC=2，
∴BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=$\sqrt{2}$OB=2$\sqrt{2}$．
故选：D．

点评本题考查了圆周角定理，等腰直角三角形．注意掌握数形结合思想的应用．

练习册系列答案

6．化简或计算：
（1）$\frac{2}{3}$$\sqrt{32}$÷（-$\frac{2}{3}$$\sqrt{6}$）×$\frac{1}{6}$$\sqrt{24}$
（2）$\sqrt{2}$×$\sqrt{32}$+${（\sqrt{2}-1）}^{2}$
（3）a-1-$\frac{{a}^{2}}{a+1}$
（4）（a-$\frac{2a-1}{a}$）÷$\frac{1{-a}^{2}}{{a}^{2}+a}$•$\frac{a-1}{{a}^{2}-2a+1}$．

3．阅读下面问题：$\frac{1}{1+\sqrt{2}}$=$\frac{1×（\sqrt{2}-1）}{（\sqrt{2}+1）（\sqrt{2}-1）}$=$\sqrt{2}$-1；$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{\sqrt{3}+\sqrt{2}}{（\sqrt{3}+\sqrt{2}）（\sqrt{3}-\sqrt{2}）}$=$\sqrt{3}$-$\sqrt{2}$；
$\frac{1}{\sqrt{5}+2}$=$\frac{\sqrt{5}-2}{（\sqrt{5}+2）（\sqrt{5}-2）}$$\sqrt{5}$-2，…．
试求：（1）$\frac{1}{\sqrt{7}+\sqrt{6}}$=$\sqrt{7}$-$\sqrt{6}$
（2）$\frac{1}{\sqrt{n+1}+\sqrt{n}}$（n为正整数）=$\sqrt{n+1}$-$\sqrt{n}$
（3）根据你发现的规律，请计算：
（$\frac{1}{{1+\sqrt{2}}}$+$\frac{1}{{\sqrt{2}+\sqrt{3}}}$+$\frac{1}{{\sqrt{3}+2}}$+…+$\frac{1}{{\sqrt{2015}+\sqrt{2016}}}$+$\frac{1}{{\sqrt{2016}+\sqrt{2017}}}$）×（1+$\sqrt{2017}$）的值．

10．

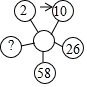如图，从左上角标注2的圆圈开始，顺时针方向按an+b的规律，（n表示前一个圆圈中的数字，a，b是常数）转换后得到下一个圆圈中的数，则标注“？”的圆圈中的数应是（　　）

20．若$\sqrt{{a}^{3}+3{a}^{2}}$=-a$\sqrt{a+3}$，则a的取值范围是（　　）

7．

如图，正方形ABCD和正三角形AEF都内接于⊙O，EF与BC，CD分别相交于点G，H，则$\frac{GH}{EF}$的值是（　　）

4．

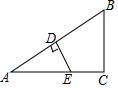如图，已知在△ABC中，∠C=90°，D是AB上一点，且BD=BC，过点D作DE⊥AB，交AC于E，若AC=4，BC=3，AB=5，则△ADE的周长等于6．

5．计算：$\sqrt{2}$（$\sqrt{12}$+4$\sqrt{\frac{1}{8}}$-$\sqrt{48}$）．

试题分类