题目内容
6.化简或计算:(1)$\frac{2}{3}$$\sqrt{32}$÷(-$\frac{2}{3}$$\sqrt{6}$)×$\frac{1}{6}$$\sqrt{24}$
(2)$\sqrt{2}$×$\sqrt{32}$+${(\sqrt{2}-1)}^{2}$
(3)a-1-$\frac{{a}^{2}}{a+1}$
(4)(a-$\frac{2a-1}{a}$)÷$\frac{1{-a}^{2}}{{a}^{2}+a}$•$\frac{a-1}{{a}^{2}-2a+1}$.
分析 (1)、(2)根据二次根式的混合运算法则进行计算即可;
(3)、(4)根据分式的混合运算法则进行计算即可.
解答 解:(1)$\frac{2}{3}$$\sqrt{32}$÷(-$\frac{2}{3}$$\sqrt{6}$)×$\frac{1}{6}$$\sqrt{24}$=-$\frac{8\sqrt{2}}{3}$×$\frac{3}{2\sqrt{6}}$×$\frac{2\sqrt{6}}{6}$=-$\frac{4\sqrt{2}}{3}$;
(2)$\sqrt{2}$×$\sqrt{32}$+${(\sqrt{2}-1)}^{2}$=8+2-2$\sqrt{2}$+1=11-2$\sqrt{2}$;
(3)a-1-$\frac{{a}^{2}}{a+1}$=$\frac{(a-1)(a+1)-{a}^{2}}{a+1}$=-$\frac{1}{a+1}$;
(4)(a-$\frac{2a-1}{a}$)÷$\frac{1{-a}^{2}}{{a}^{2}+a}$•$\frac{a-1}{{a}^{2}-2a+1}$=$\frac{{a}^{2}-2a+1}{a}$×$\frac{a(a+1)}{(1-a)(1+a)}$×$\frac{a-1}{{a}^{2}-2a+1}$=-1.
点评 此题考查了二次根式的混合运算,分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
15.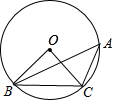 如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则BC的长为( )
如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则BC的长为( )
 如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则BC的长为( )
如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则BC的长为( )| A. | 2 | B. | 4 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
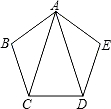 如图,在正五边形ABCDE中,AC、AD为对角线,则∠CAD的大小为36°.
如图,在正五边形ABCDE中,AC、AD为对角线,则∠CAD的大小为36°.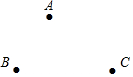 如图,已知点A、B、C.
如图,已知点A、B、C.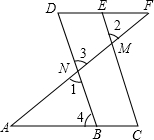 在横线上填出正确的结论,括号内写上理由已知:∠1=∠2,∠A=∠F.求证:∠C=∠D.
在横线上填出正确的结论,括号内写上理由已知:∠1=∠2,∠A=∠F.求证:∠C=∠D.