题目内容
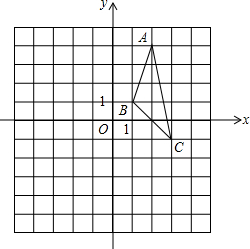 如图,在平面直角坐标系中,△ABC的三个顶点都在网格点上,回答下列问题:
如图,在平面直角坐标系中,△ABC的三个顶点都在网格点上,回答下列问题:(1)画出ABC绕点P旋转180°得到的A1B1C1,并写出点A1的坐标.
(2)画出ABC关于x轴对称的A2B2C2,并写出点A2的坐标.
(3)直接写出ABC的面积.
考点:作图-旋转变换,作图-轴对称变换
专题:
分析:(1)根据中心对称的性质找到A、B、C三点的对称点A1、B1、C1,连接A1、B1、C1即可;
(2)根据轴对称的性质找到A、B、C三点的对称点A2、B2、C2,连接A2、B2、C2即可;
(3)将△ABC的面积转化为S△ABD+S△ADC即可解答.
(2)根据轴对称的性质找到A、B、C三点的对称点A2、B2、C2,连接A2、B2、C2即可;
(3)将△ABC的面积转化为S△ABD+S△ADC即可解答.
解答:解:(1)如图1:

A1坐标为(-4,-5).
(2)如图1:A2坐标为(2,-4).
(3)如图2:

S△ABC=S△ABD+S△ADC
=
×4×1+
×4×1
=4.

A1坐标为(-4,-5).
(2)如图1:A2坐标为(2,-4).
(3)如图2:

S△ABC=S△ABD+S△ADC
=
| 1 |
| 2 |
| 1 |
| 2 |
=4.
点评:本题考查了作图--旋转变换,作图--轴对称变换,熟悉两种变换的性质是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
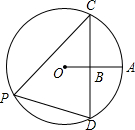 如图,点B是⊙O的半径OA的中点,且弦CD⊥OA于B,则tan∠CPD的值为( )
如图,点B是⊙O的半径OA的中点,且弦CD⊥OA于B,则tan∠CPD的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、F,连接BD交0F于点E.
如图,△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、F,连接BD交0F于点E.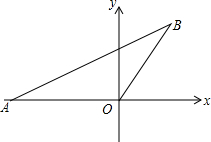 如图,OA=OB,点A的坐标是(-2,0),OB与x轴正方向夹角为60°,请画出过A,O,B三点的圆,写出圆心的坐标是
如图,OA=OB,点A的坐标是(-2,0),OB与x轴正方向夹角为60°,请画出过A,O,B三点的圆,写出圆心的坐标是 已知,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A,D,B三点,CB的延长线交⊙O于点E,延长AC至F,使得CF=CD,连接EF
已知,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A,D,B三点,CB的延长线交⊙O于点E,延长AC至F,使得CF=CD,连接EF 如图,△ABC中,AD是中线,AE是角平分线,CF垂直AE于点F,AB=5,AC=2,则FD的长是
如图,△ABC中,AD是中线,AE是角平分线,CF垂直AE于点F,AB=5,AC=2,则FD的长是