题目内容
观察下列等式:9-1=2×4,16-4=3×4,25-9=4×4,36-16=5×4,…,这些等式反映自然数间的某种规律,设n表示自然数,请猜想出这个规律,用含n的等式表示出来,并加以证明.
考点:规律型:数字的变化类
专题:
分析:先将等式进行整理,仔细观察分析整理后的等式不难发现存在的规律,用关于n的等式表示出来即可.
解答:解:将等式进行整理得:
32-12=4(1+1);
42-22=4(2+1);
52-32=4(3+1);
…
所以规律为:(n+2)2-n2=4(n+1).
证明:左边=n2+4n+4-n2=4n+4,
右边=4n+4,
左边=右边,
所以(n+2)2-n2=4(n+1).
32-12=4(1+1);
42-22=4(2+1);
52-32=4(3+1);
…
所以规律为:(n+2)2-n2=4(n+1).
证明:左边=n2+4n+4-n2=4n+4,
右边=4n+4,
左边=右边,
所以(n+2)2-n2=4(n+1).
点评:此题主要考查数字的变化规律,先对原来的等式进行整理,找出运算的规律解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
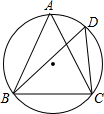 如图,在⊙O中,
如图,在⊙O中, |
| AB |
 |
| AC |
(1)求证:△ABC是等边三角形.
(2)过点B作BP∥CD,交DA延长线于点P,请依题意画出示意图.若AD=1,CD=5,求BD的长.
下列各图形中,其中的一个三角形是由另一个三角形通过平移得到的是( )
A、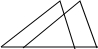 |
B、 |
C、 |
D、 |
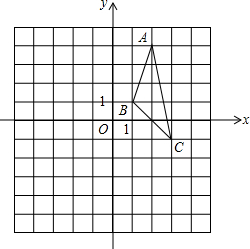 如图,在平面直角坐标系中,△ABC的三个顶点都在网格点上,回答下列问题:
如图,在平面直角坐标系中,△ABC的三个顶点都在网格点上,回答下列问题: