题目内容
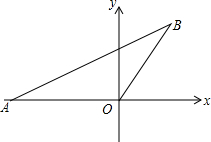如图，OA=OB，点A的坐标是（-2，0），OB与x轴正方向夹角为60°，请画出过A，O，B三点的圆，写出圆心的坐标是考点：三角形的外接圆与外心,坐标与图形性质
专题：
分析：利用三角形外心的作法进而得出AO，AB的垂直平分线进而得出圆心的位置，再利用锐角三角函数关系得出E点坐标．
解答：
解：如图所示：E点即为圆心，
∵OA=OB，点A的坐标是（-2，0），OB与x轴正方向夹角为60°，
∴∠EOA=∠BOE=60°，AF=FO=1，
故EF=tan60°FO=
，
故圆心的坐标为：（-1，
）．
故答案为：（-1，
）．
解：如图所示：E点即为圆心，∵OA=OB，点A的坐标是（-2，0），OB与x轴正方向夹角为60°，
∴∠EOA=∠BOE=60°，AF=FO=1，
故EF=tan60°FO=
| 3 |
故圆心的坐标为：（-1，
| 3 |
故答案为：（-1，
| 3 |
点评：此题主要考查了外心的性质以及坐标与图形的性质，正确结合图形得出E点位置是解题关键．
练习册系列答案
相关题目
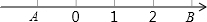如图，在数轴上有A，B两点，A，B两点表示的有理数分别是a和b，a的倒数等于它本身，|b|=3，a＜b且ab＜0．
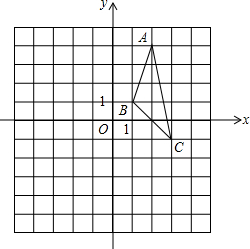如图，在平面直角坐标系中，△ABC的三个顶点都在网格点上，回答下列问题：
如图，在Rt△ABC中∠ABC=90°，以AB为直径作圆O交AC于E，连接E点和CB的中点D．
如图，在△ABC中，AB=4cm，BC=5cm，∠ABC=30°，过点A的直线α∥BC，D是直线a上一个动点，则△DBC的面积=