题目内容
5.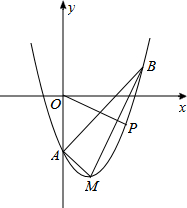 如图,在平面直角坐标系xOy中,顶点为M的抛物线是由抛物线y=x2-3向右平移一个单位后得到的,它与y轴负半轴交于点A,点B在该抛物线上,且横坐标为3.
如图,在平面直角坐标系xOy中,顶点为M的抛物线是由抛物线y=x2-3向右平移一个单位后得到的,它与y轴负半轴交于点A,点B在该抛物线上,且横坐标为3.(1)求点M、A、B坐标;
(2)连结AB、AM、BM,求∠ABM的正切值;
(3)点P是顶点为M的抛物线上一点,且位于对称轴的右侧,设PO与x正半轴的夹角为α,当α=∠ABM时,求P点坐标.
分析 (1)根据平移规律写出抛物线解析式,再求出M、A、B坐标即可.
(2)首先证明△ABE∽△AMF,推出$\frac{AM}{AB}$的值,∠BAM=90°,根据tan∠ABM=$\frac{AM}{AB}$即可解决问题.
(3)分点P在x轴上方或下方两种情形解决问题.
解答 解:(1)∵抛物线y=x2-3向右平移一个单位后得到的函数解析式为y=(x-1)2-3,
∴顶点M(1,-3),
令x=0,则y=(0-1)2-3=-2,
∴点A(0,-2),
x=3时,y=(3-1)2-3=4-3=1,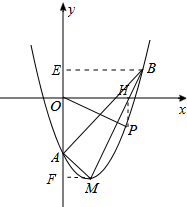
∴点B(3,1),
(2)过点B作BE⊥AO于E,过点M作MF⊥AO于M,
∵EB=EA=3,
∴∠EAB=∠EBA=45°,
同理可求∠FAM=∠FMA=45°,
∴△ABE∽△AMF,
∴$\frac{AM}{AB}$=$\frac{AF}{AE}$=$\frac{1}{3}$,
又∵∠BAM=180°-45°×2=90°,
∴tan∠ABM=$\frac{AM}{AB}$=$\frac{1}{3}$,
(3)过点P作PH⊥x轴于H,
∵y=(x-1)2-3=x2-2x-2,
∴设点P(x,x2-2x-2),
①点P在x轴的上方时,$\frac{{x}^{2}-2x-2}{x}$=$\frac{1}{3}$,
整理得,3x2-7x-6=0,
解得x1=-$\frac{2}{3}$(舍去),x2=3,
∴点P的坐标为(3,1);
②点P在x轴下方时,$\frac{-({x}^{2}-2x-2)}{x}$=$\frac{1}{3}$,
整理得,3x2-5x-6=0,
解得x1=$\frac{5-\sqrt{97}}{6}$(舍去),x2=$\frac{5+\sqrt{97}}{6}$,x=$\frac{5+\sqrt{97}}{6}$时,y=x2-2x-2=$-\frac{{5+\sqrt{97}}}{18}$,
∴点P的坐标为($\frac{{5+\sqrt{97}}}{6}$,$-\frac{{5+\sqrt{97}}}{18}$),
综上所述,点P的坐标为(3,1)或($\frac{{5+\sqrt{97}}}{6}$,$-\frac{{5+\sqrt{97}}}{18}$).
点评 本题考查二次函数综合题、相似三角形的判定和性质、锐角三角函数、待定系数法等知识,解题的关键是掌握平移规律,学会添加常用辅助线,构造相似三角形解决问题,学会分类讨论,注意考虑问题要全面,属于中考压轴题.

| 种类 | A选项 | B选项 | C选项 | D选项 | E选项 | F选项 |
| 实施“二孩”的可能变化 | 延缓社会老龄化 | 家庭发展能力提升 | 导致人口暴增 | 增加公共资源压力 | 出生人口性别趋衡 | 劳动年龄人口增加 |
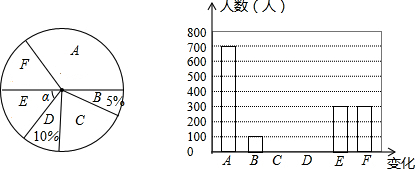
根据统计图,回答下列问题:
(1)参与调查的市民一共有2000人;
(2)请补全条形统计图;
(3)求∠α;
(4)若该区有155万常住人口,对于二孩政策的实施给生活带来的变化,请估计该区有多少万人会选择B选项“家庭发展能力提升”?
| A. | 2a2+a=3a3 | B. | (m2)3=m5 | C. | (x+y)2=x2+y2 | D. | a6÷a3=a3 |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
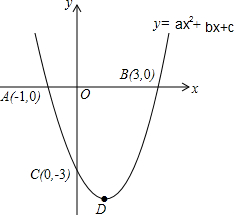 如图,抛物线y=ax2+bx+c的图象与x轴交于A(-1.0),B(3,0)两点,与y轴交于点C(0,-3),顶点为D.
如图,抛物线y=ax2+bx+c的图象与x轴交于A(-1.0),B(3,0)两点,与y轴交于点C(0,-3),顶点为D.


