题目内容
16. 已知:如图,AB是⊙O的直径,直线l交⊙O于C、D两点,AE⊥l,BF⊥l,E、F是垂足,求证:EC=DF.
已知:如图,AB是⊙O的直径,直线l交⊙O于C、D两点,AE⊥l,BF⊥l,E、F是垂足,求证:EC=DF.
分析 过点O作OM⊥CD于点M,根据垂径定理可知CM=DM,再由AE⊥l,OM⊥l,BF⊥l可得出AE∥OM∥BF,再根据AB是⊙O的直径可知OA=OB,故OM是梯形AEFB的中位线,再由EM-CM=FM-DM即可得出结论.
解答 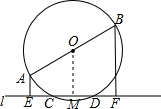 证明:过点O作OM⊥CD于点M,
证明:过点O作OM⊥CD于点M,
∵OM⊥CD,
∴CM=DM,
∵AE⊥l,OM⊥l,BF⊥l,
∴AE∥OM∥BF,
∵AB是⊙O的直径,
∴OA=OB,
∴OM是梯形AEFB的中位线,
∴EM=FM
∴EM-CM=FM-DM,即EC=DF
点评 本题考查的是垂径定理,根据题意作出辅助线,利用垂径定理及梯形中位线定理求解是解答此题的关键.

练习册系列答案
相关题目
5. 下面四个艺术字中,是轴对称图形的个数是( )
下面四个艺术字中,是轴对称图形的个数是( )
 下面四个艺术字中,是轴对称图形的个数是( )
下面四个艺术字中,是轴对称图形的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,在直角坐标系中,已知A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
如图,在直角坐标系中,已知A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.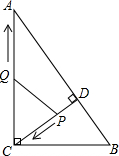 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到点C时,两点都停止.设运动时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到点C时,两点都停止.设运动时间为t秒. 如图,在△ABC中,AB=AC,EF交AB于点E,交BC与点D.交AC的延长线于点F,且BE=CF.求证:DE=DF.
如图,在△ABC中,AB=AC,EF交AB于点E,交BC与点D.交AC的延长线于点F,且BE=CF.求证:DE=DF. 如图所示,已知∠ACB=90°,∠ADC=90°,图中互相垂直的线段有AC⊥BC,CD⊥AB.
如图所示,已知∠ACB=90°,∠ADC=90°,图中互相垂直的线段有AC⊥BC,CD⊥AB.