题目内容
13.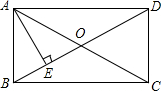 如图,在矩形ABCD中,AE⊥BD于E,AC与BD相交于O点,DE=3BE.
如图,在矩形ABCD中,AE⊥BD于E,AC与BD相交于O点,DE=3BE.(1)求∠1的度数;
(2)若AD=12cm,求AE、AB的长.
分析 (1)由矩形的性质得出OB=OD=$\frac{1}{2}$BD,OA=OC=$\frac{1}{2}$AC,AC=BD,证出OA=OB,易证得△OAB是等边三角形,继而求得∠1的度数;
(2)由△OAB是等边三角形,易求得∠ADE=30°,又由AD=12cm,由含30°角的直角三角形的性质求得AE的长,由三角函数求出AB的长即可.
解答 解:(1)∵四边形ABCD是矩形,
∴OB=OD=$\frac{1}{2}$BD,OA=OC=$\frac{1}{2}$AC,AC=BD,
∴OA=OB,
∵DE=3BE,
∴BE=OE,
∵AE⊥BD,
∴AB=OA,
∴OA=AB=OB,
即△OAB是等边三角形,
∴∠BAO=60°,
∴∠1=$\frac{1}{2}$∠BAO=30°;
(2)∵△OAB是等边三角形,
∴∠ABD=60°,
∴∠ADE=90°-∠ABD=30°,
∵AE⊥BD,AD=12cm,
∴AE=$\frac{1}{2}$AD=6cm,AB=AD•tan30°=12×$\frac{\sqrt{3}}{3}$=4$\sqrt{3}$(cm).
点评 此题考查了矩形的性质、等边三角形的判定与性质、含30°角的直角三角形的性质、三角函数.此题难度不大,证明△AOB是等边三角形是解决问题的关键.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
3. 抛物线y=-x2+bx+c的部分图象如图所示,对称轴是直线x=-1,与x轴交于点(1,0),若y<0,则x的取值范围是( )
抛物线y=-x2+bx+c的部分图象如图所示,对称轴是直线x=-1,与x轴交于点(1,0),若y<0,则x的取值范围是( )
 抛物线y=-x2+bx+c的部分图象如图所示,对称轴是直线x=-1,与x轴交于点(1,0),若y<0,则x的取值范围是( )
抛物线y=-x2+bx+c的部分图象如图所示,对称轴是直线x=-1,与x轴交于点(1,0),若y<0,则x的取值范围是( )| A. | x>0 | B. | x>1 | C. | x<-3或x>1 | D. | D-3<x<1 |
5. 下面四个艺术字中,是轴对称图形的个数是( )
下面四个艺术字中,是轴对称图形的个数是( )
 下面四个艺术字中,是轴对称图形的个数是( )
下面四个艺术字中,是轴对称图形的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,在△ABC中,AB=AC,EF交AB于点E,交BC与点D.交AC的延长线于点F,且BE=CF.求证:DE=DF.
如图,在△ABC中,AB=AC,EF交AB于点E,交BC与点D.交AC的延长线于点F,且BE=CF.求证:DE=DF. 如图,在ABC中,∠A=∠B=30°,过点C作CD⊥AC,交AB于点D.
如图,在ABC中,∠A=∠B=30°,过点C作CD⊥AC,交AB于点D. 如图,在∠1,∠2,∠3,∠4,∠5中,是同位角的是∠1与∠4;是内错角的是∠5与∠2、∠3与∠2;同旁内角的是∠1与∠5、∠3与∠4.
如图,在∠1,∠2,∠3,∠4,∠5中,是同位角的是∠1与∠4;是内错角的是∠5与∠2、∠3与∠2;同旁内角的是∠1与∠5、∠3与∠4.