题目内容
19. 如图,在△ABC中,AB=AC,∠A=30°,以C为圆心,CB的长为半径作圆弧,交AB于点D,连接CD,则∠ACD等于( )
如图,在△ABC中,AB=AC,∠A=30°,以C为圆心,CB的长为半径作圆弧,交AB于点D,连接CD,则∠ACD等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
分析 根据等腰三角形两底角相等求出∠ABC=∠ACB,再求出∠BCD,然后根据∠ACD=∠ABC-∠BCD计算即可得解.
解答 解:∵AB=AC,∠A=30°,
∴∠ACB=∠ABC=$\frac{1}{2}$(180°-∠A)=$\frac{1}{2}$(180°-30°)=75°,
∵以C为圆心,BC的长为半径圆弧,交AC于点D,
∴BC=CD,
∴∠BCD=180°-2∠ACB=180°-2×75°=30°,
∴∠ACD=∠ABC-∠BCD=75°-30°=45°.
故选:B.
点评 本题考查了等腰三角形的性质,主要利用了等腰三角形两底角相等,熟记性质是解题的关键.

练习册系列答案
相关题目
14. 如图,在△ABC中,AB=AC,∠A=25°,DE垂直平分AC,交AB于点D,连接CD,则∠BCD的度数为( )
如图,在△ABC中,AB=AC,∠A=25°,DE垂直平分AC,交AB于点D,连接CD,则∠BCD的度数为( )
 如图,在△ABC中,AB=AC,∠A=25°,DE垂直平分AC,交AB于点D,连接CD,则∠BCD的度数为( )
如图,在△ABC中,AB=AC,∠A=25°,DE垂直平分AC,交AB于点D,连接CD,则∠BCD的度数为( )| A. | 50° | B. | 25° | C. | 52.5° | D. | 无法确定 |
 如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,点D为AC边上的动点,点D从点C出发,沿边CA向A运动,当运动到点A时停止,若设点D运动的速度为每秒1个单位长度,当运动时间t为多少秒时,以点C、B、D为顶点的三角形是等腰三角形?
如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,点D为AC边上的动点,点D从点C出发,沿边CA向A运动,当运动到点A时停止,若设点D运动的速度为每秒1个单位长度,当运动时间t为多少秒时,以点C、B、D为顶点的三角形是等腰三角形?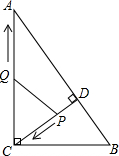 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到点C时,两点都停止.设运动时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到点C时,两点都停止.设运动时间为t秒. 如图,在△ABC中,AB=AC,EF交AB于点E,交BC与点D.交AC的延长线于点F,且BE=CF.求证:DE=DF.
如图,在△ABC中,AB=AC,EF交AB于点E,交BC与点D.交AC的延长线于点F,且BE=CF.求证:DE=DF. 如图,该平面展开图按虚线折叠成正方体后,相对面上两个数之和为8,则x+y=10.
如图,该平面展开图按虚线折叠成正方体后,相对面上两个数之和为8,则x+y=10.