题目内容
18.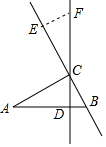 如图,Rt△ABC中,直角边AC=7cm,BC=3cm,CD为斜边AB上的高,点E从点B出发沿直线BC以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.
如图,Rt△ABC中,直角边AC=7cm,BC=3cm,CD为斜边AB上的高,点E从点B出发沿直线BC以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.(1)求证:∠A=∠BCD;
(2)点E运动多长时间,CF=AB?并说明理由.
分析 (1)根据余角的性质即可得到结论;
(2)如图,当点E在射线BC上移动时,若E移动5s,则BE=2×5=10cm,根据全等三角形的判定和性质即可得到结论.
解答 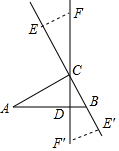 解:(1)∵∠A+∠ACD=90°,∠BCD+∠ACD=90°,
解:(1)∵∠A+∠ACD=90°,∠BCD+∠ACD=90°,
∴∠A=∠BCD,
(2)如图,当点E在射线BC上移动时,若E移动5s,则BE=2×5=10cm,
∴CE=BE-BC=10-3=7cm.
∴CE=AC,
在△CFE与△ABC中$\left\{\begin{array}{l}{∠ECF=∠A}\\{CE=AC}\\{∠CEF=∠ACD}\end{array}\right.$,
∴△CEF≌△ABC,
∴CF=AB,
当点E在射线CB上移动时,若E移动2s,则BE′=2×2=4cm,
∴CE′=BE′+BC=4+3=7cm,
∴CE′=AC,
在△CF′E′与△ABC中$\left\{\begin{array}{l}{∠E′CF=∠A}\\{CE′=AC}\\{∠CEF′=∠ACD=90°}\end{array}\right.$,
∴△CF′E′≌△ABC,
∴CF′=AB,
总之,当点E在射线CB上移动5s,或2s时,CF′=AB.
点评 本题考查了全等三角形的判定和性质,余角的性质,熟练正确全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
8.某帐篷集团的总厂和分厂分别位于甲、乙两市,两厂原来每周生产帐篷共11千顶,“芦山地震”发生后,灾区A、B急需帐篷20千顶,该集团决定在一周内赶制出这批帐篷.总厂和分厂的生产效率分别比原来提高了100%和50%,恰好按时完成了这项任务.
(1)在赶制帐篷的一周内,总厂和分厂各生产帐篷多少千顶?
(2)现要将这些帐篷用卡车一次性运送到该地震灾区的A,B两地,由于甲、乙两市通住A,B两地的情况不同,卡车的运载量也不同.已知运送帐篷每千顶所需的车辆数和两地所急需的帐篷数如表:
请设计一种运送方案,使所需的车辆总数最少.说明理由,并求出最少车辆总数.
(1)在赶制帐篷的一周内,总厂和分厂各生产帐篷多少千顶?
(2)现要将这些帐篷用卡车一次性运送到该地震灾区的A,B两地,由于甲、乙两市通住A,B两地的情况不同,卡车的运载量也不同.已知运送帐篷每千顶所需的车辆数和两地所急需的帐篷数如表:
| A地 | B地 | ||
| 每千顶帐篷 所需车辆数(单位:辆) | 甲市 | 4 | 7 |
| 乙市 | 3 | 5 | |
| 急需帐篷数(单位:千顶) | 9 | 11 | |
9.①要调查一批灯泡的使用寿命,②要对“神州十号”飞船零件质量进行检查,应采用( )
| A. | 都是普查 | B. | 都是抽查 | C. | ①是普查②是抽查 | D. | ①是抽查②是普查 |
6.下列各式从左到右的变形一定正确的是( )
| A. | $\frac{2}{3}$=$\frac{2a}{3a}$ | B. | $\frac{3a}{3b}$=$\frac{a}{b}$ | C. | $\frac{a}{b}$=$\frac{a+1}{b+1}$ | D. | $\frac{a}{b}$=$\frac{{a}^{2}}{{b}^{2}}$ |
3.下列各式:$\frac{2}{x}$、$\frac{x+2}{2}$、$\frac{x-xy}{x}$、3x+$\frac{y}{3}$、$\frac{3x}{π+2}$、$\frac{3{x}^{2}-4}{0.5}$中,分式有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.计算机是将信息转换成二进制数进行处理的,二进制即“逢2进1”,如(1101)2表示二进制数,将它转换成十进制形式是1×23+1×22+0×21+1×20=13,那么将二进制(1111)2转换成十进制形式是( )
| A. | 8 | B. | 15 | C. | 30 | D. | 31 |
7.已知m+n=2,mn=-2,则(2-m)(2-n)的值为( )
| A. | 2 | B. | -2 | C. | 0 | D. | 3 |
8.一次函数y=$\frac{4}{3}$x-b沿y轴平移3个单位得直线与y=$\frac{4}{3}$x-1,则b的值为( )
| A. | -2或4 | B. | 2或-4 | C. | 4或-6 | D. | -4或6 |