题目内容
7．已知m+n=2，mn=-2，则（2-m）（2-n）的值为（ ）| A． | 2 | B． | -2 | C． | 0 | D． | 3 |
分析 根据多项式乘以多项式的法则将原式展开，然后条件即可求出原式的值．
解答 解：（2-m）（2-n）=4-2（m+n）+mn
∵m+n=2，mn=-2
∴原式=4-4-2=-2
故选（B）
点评 本题考查多项式乘以多项式，解题的关键是熟练运用整式的运算法则，本题属于基础题型．
练习册系列答案
相关题目
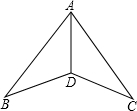如图，峰峰先在一家白纸上用直尺画出了相等的线段AB和AC，然后用量角器作出了度数都为30°的∠ABD和∠ACD，最后连接AD，此时他就断定AD是∠BAC的平分线，你同意他的结论吗？如果同意，请证明；如果不同意，请说明理由．
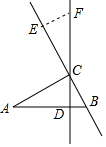如图，Rt△ABC中，直角边AC=7cm，BC=3cm，CD为斜边AB上的高，点E从点B出发沿直线BC以2cm/s的速度移动，过点E作BC的垂线交直线CD于点F．
15．下列计算正确的是（ ）
| A． | a3•a2=a6 | B． | a3-a2=a | C． | （-a3）2=a6 | D． | a6÷a2=a3 |
2．如果一个三角形的两边长分别为3和7，则第三边长可能是（ ）
| A． | 3 | B． | 4 | C． | 7 | D． | 10 |
12．分式方程$\frac{x}{x+2}$=$\frac{1}{2}$的解是（ ）
| A． | x=1 | B． | x=-1 | C． | x=2 | D． | x=-2 |
17．若关于x的分式方程$\frac{x}{x-3}$=2-$\frac{m}{3-x}$有增根，则m的值为（ ）
| A． | -3 | B． | 2 | C． | 3 | D． | 不存在 |