题目内容
8.某帐篷集团的总厂和分厂分别位于甲、乙两市,两厂原来每周生产帐篷共11千顶,“芦山地震”发生后,灾区A、B急需帐篷20千顶,该集团决定在一周内赶制出这批帐篷.总厂和分厂的生产效率分别比原来提高了100%和50%,恰好按时完成了这项任务.(1)在赶制帐篷的一周内,总厂和分厂各生产帐篷多少千顶?
(2)现要将这些帐篷用卡车一次性运送到该地震灾区的A,B两地,由于甲、乙两市通住A,B两地的情况不同,卡车的运载量也不同.已知运送帐篷每千顶所需的车辆数和两地所急需的帐篷数如表:
| A地 | B地 | ||
| 每千顶帐篷 所需车辆数(单位:辆) | 甲市 | 4 | 7 |
| 乙市 | 3 | 5 | |
| 急需帐篷数(单位:千顶) | 9 | 11 | |
分析 (1)有两个等量关系:原来总厂每周生产帐篷数+分厂每周生产帐篷数=9千,现在总厂每周生产帐篷数+分厂每周生产帐篷数=14千,直接设未知数,可以根据等量关系列出二元一次方程组解决问题.
(2)首先应考虑到影响车辆总数的因素有两个,帐篷顶数和每千顶帐篷所需车辆数,所需车辆总数是两者的积;其次应考虑到由总厂,分厂运送到A,B两地的帐篷数共四个量,即总厂--A,总厂--B,分厂--A,分厂--B的帐篷数,它们互相联系.
解答 解:(1)设原来总厂每周生产帐篷数x千顶,分厂每周生产帐篷数y千顶.
由题意$\left\{\begin{array}{l}{x+y=11}\\{2x+1.5y=20}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=7}\\{y=4}\end{array}\right.$,
2×7=14,4×1.5=6,
答:在赶制帐篷的一周内,总厂和分厂分别生产帐篷14千顶和6千顶.
(2)设从(甲市)总厂调配m千顶帐篷到灾区的A地,则总厂调配到灾区B地的帐篷为(14-m)千顶,
(乙市)分厂调配到灾区A,B两地的帐篷分别为(9-m),(m-3)千顶.
甲、乙两市所需运送帐篷的车辆总数为n辆.
由题意得:n=4m+7(14-m)+3(9-m)+5(m-3)(3≤m≤9).
即:n=-m+110(3≤m≤9).
因为-1<0,所以n随m的增大而减小.
所以当m=9时,n有最小值101.
答:从总厂运送到灾区A、B两地帐篷分别帐篷9千顶、5千顶,从分厂运送到灾区A,B两地帐篷分别为0千顶、6千顶时所用车辆最少,最少的车辆为101辆.
点评 本题考查一次函数的应用、二元一次方程组等知识,解决含有多个变量的问题时,可以分析这些多个变量之间的关系,从中选取有代表性的变量作为自变量,然后根据问题的条件寻求可以反映实际问题的函数,以此作为解决问题的数学模型.

 名校课堂系列答案
名校课堂系列答案

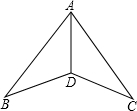 如图,峰峰先在一家白纸上用直尺画出了相等的线段AB和AC,然后用量角器作出了度数都为30°的∠ABD和∠ACD,最后连接AD,此时他就断定AD是∠BAC的平分线,你同意他的结论吗?如果同意,请证明;如果不同意,请说明理由.
如图,峰峰先在一家白纸上用直尺画出了相等的线段AB和AC,然后用量角器作出了度数都为30°的∠ABD和∠ACD,最后连接AD,此时他就断定AD是∠BAC的平分线,你同意他的结论吗?如果同意,请证明;如果不同意,请说明理由.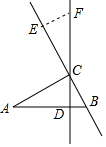 如图,Rt△ABC中,直角边AC=7cm,BC=3cm,CD为斜边AB上的高,点E从点B出发沿直线BC以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.
如图,Rt△ABC中,直角边AC=7cm,BC=3cm,CD为斜边AB上的高,点E从点B出发沿直线BC以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.