题目内容
13.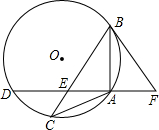 已知:如图,△ABC中,内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.
已知:如图,△ABC中,内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.(1)求证:BF与⊙O相切;
(2)若BF=5,cosC=$\frac{4}{5}$,求⊙O的半径.
分析 (1)连接BD,证明BF是⊙O的切线,只需证明∠FBD=90°;
(2)由Rt△BDF中的勾股定理进行解答即可.
解答 证明:(1)连接BD,
∵AD⊥AB,
∴∠BAD=90°,
∴BD是直径,BD过圆心,
∵AB=AC,
∴∠ABC=∠D,
又∵∠C=∠D,
∴△BEF是等腰三角形,
∴∠ABC=∠ABF,
∴∠D=∠ABF,
又∵∠BAD=90°,
∴∠ABD+∠D
=180°-∠BAD
=180°-90°
=90°,
∴∠ABD+∠ABF=90°,
∴∠DBF=90°,
∴OB⊥BF,
又∵OB是⊙O的半径,
∴BF是⊙OA切线;
(2)∵∠C=∠D,
∴cosD=cosC=$\frac{4}{5}$,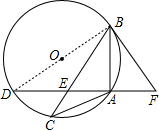
在Rt△BDF中
cosD=$\frac{BD}{DF}=\frac{4}{5}$,
∴设BD=4x,DF=5x,
又∵BD2+BF2=DF2
∴(4x)2+52=(5x)2
x=$\frac{25}{9}$,
∵x>0
∴x=$\frac{5}{3}$,
∴BD=4×$\frac{5}{3}$=$\frac{20}{3}$,
∴OB=$\frac{1}{2}$BD=$\frac{10}{3}$
∴⊙O半径为$\frac{10}{3}$.
点评 本题考查圆的切线的判断,关键是证明∠FBD=90°来证明BF是⊙O的切线.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
18.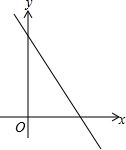 已知x关于的一次函数y=mx+n的图象如上图,则|n-m|-$\sqrt{m^2}+\sqrt{{{(m-n)}^2}}$可化简( )
已知x关于的一次函数y=mx+n的图象如上图,则|n-m|-$\sqrt{m^2}+\sqrt{{{(m-n)}^2}}$可化简( )
 已知x关于的一次函数y=mx+n的图象如上图,则|n-m|-$\sqrt{m^2}+\sqrt{{{(m-n)}^2}}$可化简( )
已知x关于的一次函数y=mx+n的图象如上图,则|n-m|-$\sqrt{m^2}+\sqrt{{{(m-n)}^2}}$可化简( )| A. | n | B. | n-2m | C. | m | D. | 2n-m |
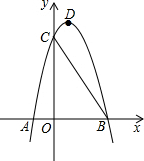 如图,已知抛物线y=ax2+bx+8(a≠0)与x轴交于点A(-2,0),B,与y轴交于点C,tan∠ABC=2.
如图,已知抛物线y=ax2+bx+8(a≠0)与x轴交于点A(-2,0),B,与y轴交于点C,tan∠ABC=2.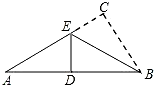 在Rt△ABC中,∠C=90°,当△ABC沿折痕BE翻折时,点C恰好落在AB的中点D上,若BE=4,则AC的长是( )
在Rt△ABC中,∠C=90°,当△ABC沿折痕BE翻折时,点C恰好落在AB的中点D上,若BE=4,则AC的长是( ) 如图,在△ABC中,∠B=40°,过点C作CD∥AB,∠ACD=65°,则∠ACB的度数为75°.
如图,在△ABC中,∠B=40°,过点C作CD∥AB,∠ACD=65°,则∠ACB的度数为75°. 如图,在平面直角坐标系中,所有小方格的边长都为1个单位长度.
如图,在平面直角坐标系中,所有小方格的边长都为1个单位长度.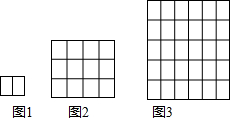 这样铺地板:第一块铺2块,如图1,第二次把第一次的完全围起来,如图2;第三次把第二次的完全围起来,如图3;…依次方法,铺第5次时需用34块木块才能把第四次所铺的完全围起来.
这样铺地板:第一块铺2块,如图1,第二次把第一次的完全围起来,如图2;第三次把第二次的完全围起来,如图3;…依次方法,铺第5次时需用34块木块才能把第四次所铺的完全围起来.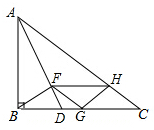 Rt△ABC,∠ABC=90°,AD平分∠BAC,BF⊥AC交AD于F,FH∥BC交于H,FG∥AC
Rt△ABC,∠ABC=90°,AD平分∠BAC,BF⊥AC交AD于F,FH∥BC交于H,FG∥AC