题目内容
1.若方程x2m+n-9+y3m-n-6=0是关于x,y的二元一次方程,则mn=$\frac{272}{25}$.分析 二元一次方程满足的条件:含有2个未知数,未知数的项的次数是1的整式方程.
解答 解:由x2m+n-9+y3m-n-6=0是关于x,y的二元一次方程,得
$\left\{\begin{array}{l}{2m+n-9=1}\\{3m-n-6=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=\frac{17}{5}}\\{n=\frac{16}{5}}\end{array}\right.$,
mn=$\frac{17}{5}$×$\frac{16}{5}$=$\frac{272}{25}$.
故答案为:$\frac{272}{25}$.
点评 主要考查二元一次方程的概念,要求熟悉二元一次方程的形式及其特点:含有2个未知数,未知数的项的次数是1的整式方程.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.-$\frac{3}{4}$的绝对值是( )
| A. | $-\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $-\frac{4}{3}$ | D. | $\frac{4}{3}$ |
 如图,点E在边长为4的正方形ABCD的边AD上,点A关于BE的对称点为A′,延长EA′交DC于点F,若CF=1cm,则AE=2.4cm.
如图,点E在边长为4的正方形ABCD的边AD上,点A关于BE的对称点为A′,延长EA′交DC于点F,若CF=1cm,则AE=2.4cm.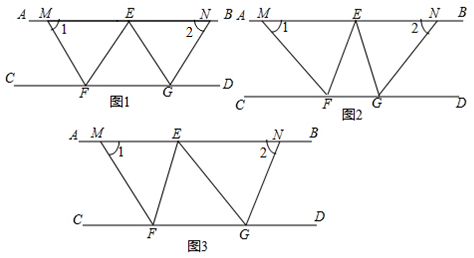
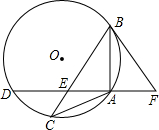 已知:如图,△ABC中,内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.
已知:如图,△ABC中,内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.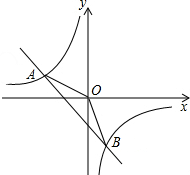 如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$图象交于A(-2,1)、B(n,-2)两点.
如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$图象交于A(-2,1)、B(n,-2)两点.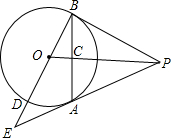 如图,PA为⊙O的切线,A为切点,过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点B,延长BO与⊙O交于点D,与PA的延长线交于点E,
如图,PA为⊙O的切线,A为切点,过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点B,延长BO与⊙O交于点D,与PA的延长线交于点E,