题目内容
4.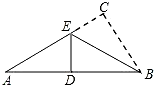 在Rt△ABC中,∠C=90°,当△ABC沿折痕BE翻折时,点C恰好落在AB的中点D上,若BE=4,则AC的长是( )
在Rt△ABC中,∠C=90°,当△ABC沿折痕BE翻折时,点C恰好落在AB的中点D上,若BE=4,则AC的长是( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
分析 根据翻折变换的性质得到∠EDB=∠C=90°,∠EBA=∠EBC,根据垂直平分线的性质得到EA=EB,根据等腰三角形的性质求出∠EBC=30°,根据直角三角形的性质解答即可.
解答 解:由翻折变换的性质可知,∠EDB=∠C=90°,∠EBA=∠EBC,
∵D是AB的中点,
∴EA=EB=4,
∴∠EBA=∠A,
∴∠EBA=∠A=∠EBC=30°,
∴EC=$\frac{1}{2}$EB=2,
∴AC=AE+EC=6,
故选:B.
点评 本题考查的是翻折变换的性质,翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
19.不等式2x-2<0的解集是( )
| A. | x<1 | B. | x<-1 | C. | x>1 | D. | x>-1 |
 如图,若∠1=40°,∠2=40°,∠3=120°,则∠4=60°.
如图,若∠1=40°,∠2=40°,∠3=120°,则∠4=60°. 如图,点E在边长为4的正方形ABCD的边AD上,点A关于BE的对称点为A′,延长EA′交DC于点F,若CF=1cm,则AE=2.4cm.
如图,点E在边长为4的正方形ABCD的边AD上,点A关于BE的对称点为A′,延长EA′交DC于点F,若CF=1cm,则AE=2.4cm.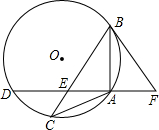 已知:如图,△ABC中,内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.
已知:如图,△ABC中,内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.